
分析 由函数奇偶性的定义判断①;直接求出函数的值域判断②;求出满足A∪B=A的a的值判断③;由偶函数的性质结合f(2-m)<f(m)求得m的范围判断④;求出使函数定义域为R的k的范围判断⑤.
解答 解:①函数$f(x)=x+\frac{1}{x}$的定义域为R,且f(-x)=-x-$\frac{1}{x}=-f(x)$,函数为奇函数,①正确;
②∵3-2x-x2=-(x+1)2+4≤4,∴0≤$\sqrt{3-2x-{x}^{2}}$≤2,函数$y=\sqrt{3-2x-{x^2}}$的值域为{y|0≤y≤2},②错误;
③集合A={-1,3},B={x|ax-1=0,a∈R},若A∪B=A,则B⊆A.
a=0时,B=∅满足;a≠0时,B={$\frac{1}{a}$},∴$\frac{1}{a}=-1$或$\frac{1}{a}=3$,即a=-1或a=$\frac{1}{3}$.
∴a的取值集合为{0,-1,$\frac{1}{3}$},③错误;
④定义在R上的偶函数f(x)在[0,+∞)上单调递减,且f(2-m)<f(m),则|2-m|>|m|,解得m∈(-∞,1),④正确;
⑤若函数$f(x)=\frac{1}{{\sqrt{({k^2}+4k-5){x^2}-4(k-1)x+3}}}$的定义域为R,则(k2+4k-5)x2-4(k-1)x+3>0对任意实数x恒成立.
当k=1时成立;当k≠1时,则$\left\{\begin{array}{l}{{k}^{2}+4k-5>0}\\{16(k-1)^{2}-12({k}^{2}+4k-5)<0}\end{array}\right.$,解得k∈[1,19),⑤错误.
∴正确命题的序号是①④⑤.
故答案为:①④⑤.
点评 本题考查命题的真假判断与应用,考查了函数的性质,训练了函数定义域的求法,属中档题.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | 5 | C. | 2 | D. | $\frac{5}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
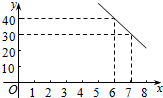 某公司试销一种成本单价为50元/件的新产品,规定试销时销售单价不低于成本单价,又不高于80元/件.经试销调查,发现销售量y(件)与销售单价x(元/件)可近似看作一次函数y=kx+b的关系(如图所示).
某公司试销一种成本单价为50元/件的新产品,规定试销时销售单价不低于成本单价,又不高于80元/件.经试销调查,发现销售量y(件)与销售单价x(元/件)可近似看作一次函数y=kx+b的关系(如图所示).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x>$\frac{x+y}{2}$>$\sqrt{xy}$>y | B. | y>$\frac{x+y}{2}$>$\sqrt{xy}$>x | C. | x>$\frac{x+y}{2}$>y>$\sqrt{xy}$ | D. | y>$\frac{x+y}{2}$≥$\sqrt{xy}$>x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{3}{8}$,-$\frac{1}{8}$) | B. | (-$\frac{3}{8}$,$\frac{1}{8}$) | C. | ($\frac{3}{10}$,-$\frac{1}{10}$) | D. | ($\frac{3}{10}$,$\frac{1}{10}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com