
正方形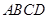 的边长为2,
的边长为2,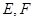 分别为边
分别为边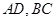 的中点,
的中点,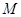 是线段
是线段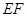 的中点,如图,把正方形沿
的中点,如图,把正方形沿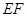 折起,设
折起,设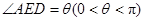 .
.
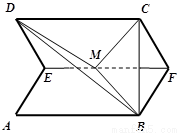
(1)求证:无论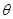 取何值,
取何值,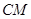 与
与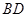 不可能垂直;
不可能垂直;
(2)设二面角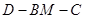 的大小为
的大小为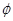 ,当
,当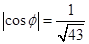 时,求
时,求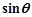 的值.
的值.
(1)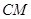 与
与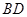 不可能垂直; (2)
不可能垂直; (2)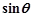 的值为
的值为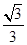 .
.
【解析】
试题分析:(1)假设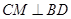 , 1分
, 1分
又因为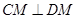 ,
,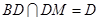 ,所以
,所以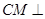 平面
平面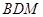 ,
3分
,
3分
所以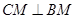 ,又
,又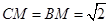 ,所以
,所以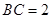 , 5分
, 5分
这与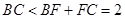 矛盾,所以假设不成立,所以
矛盾,所以假设不成立,所以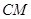 与
与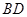 不可能垂直; 6分
不可能垂直; 6分
(2)分别以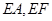 为
为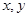 轴,过点
轴,过点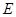 垂直平面
垂直平面 向上为
向上为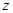 轴,如图建立坐标系,
轴,如图建立坐标系,
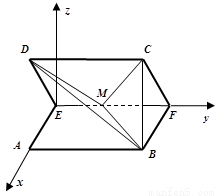
设平面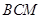 的一个法向量为
的一个法向量为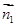 ,
,
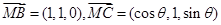 ,
,
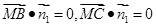 , 7分
, 7分
得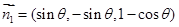 , 8分
, 8分
设平面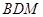 的一个法向量为
的一个法向量为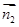 ,
,
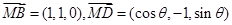 ,
,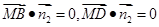 , 9分
, 9分
得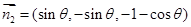 , 10分
, 10分
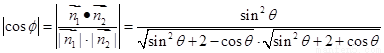 11分
11分
=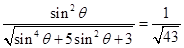 , 12分
, 12分
得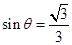 , 13分
, 13分
所以当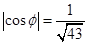 时,
时,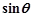 的值为
的值为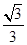 . 14分
. 14分
考点:折叠问题,平行关系,垂直关系,角的计算。
点评:中档题,立体几何问题中,平行关系、垂直关系,角、距离、面积、体积等的计算,是常见题型,基本思路是将空间问题转化成为平面问题,利用平面几何知识加以解决。要注意遵循“一作,二证,三计算”。利用“向量法”,通过建立空间直角坐标系,往往能简化解题过程。对于折叠问题,首先要弄清“变”与“不变”的几何元素。


科目:高中数学 来源: 题型:
 如图所示,过正方形ABCD的中心O作OP⊥平面ABCD,已知正方形的边长为2,OP=2,连接AP、BP、CP、DP,M、N分别是AB、BC的中点,以O为原点,射线OM、ON、OP分别为Ox轴、Oy轴、Oz轴的正方向建立空间直角坐标系.若E、F分别为PA、PB的中点,求A、B、C、D、E、F的坐标.
如图所示,过正方形ABCD的中心O作OP⊥平面ABCD,已知正方形的边长为2,OP=2,连接AP、BP、CP、DP,M、N分别是AB、BC的中点,以O为原点,射线OM、ON、OP分别为Ox轴、Oy轴、Oz轴的正方向建立空间直角坐标系.若E、F分别为PA、PB的中点,求A、B、C、D、E、F的坐标.查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省广州市毕业班综合测试(二)理科数学试卷(解析版) 题型:解答题
已知正方形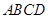 的边长为2,
的边长为2,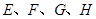 分别是边
分别是边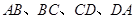 的中点.
的中点.
(1)在正方形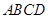 内部随机取一点
内部随机取一点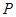 ,求满足
,求满足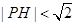 的概率;
的概率;
(2)从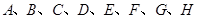 这八个点中,随机选取两个点,记这两个点之间的距离为
这八个点中,随机选取两个点,记这两个点之间的距离为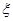 ,求随机变量
,求随机变量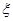 的分布列与数学期望
的分布列与数学期望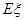 .
.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西省高三最后一次模拟考试文科数学试卷(解析版) 题型:解答题
已知正方形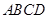 的边长为2,
的边长为2,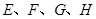 分别是边
分别是边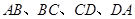 的中点.
的中点.
(1)在正方形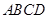 内部随机取一点
内部随机取一点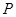 ,求满足
,求满足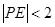 的概率;
的概率;
(2)从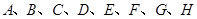 这八个点中,随机选取两个点,记这两个点之间的距离的平方为
这八个点中,随机选取两个点,记这两个点之间的距离的平方为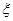 ,求
,求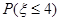 .
.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年深圳市高三第一次调研考试数学文卷 题型:解答题
(本题满分12分)
如图,有一正方形钢板 缺损一角(图中的阴影部分),边缘线
缺损一角(图中的阴影部分),边缘线 是以直线AD为对称轴,以线段
是以直线AD为对称轴,以线段 的中点
的中点 为顶点的抛物线的一部分.工人师傅要将缺损一角切割下来,使剩余的部分成为一个直角梯形.若正方形的边长为2米,问如何画切割线
为顶点的抛物线的一部分.工人师傅要将缺损一角切割下来,使剩余的部分成为一个直角梯形.若正方形的边长为2米,问如何画切割线 ,可使剩余的直角梯形的面积最大?并求其最大值.
,可使剩余的直角梯形的面积最大?并求其最大值.

查看答案和解析>>
科目:高中数学 来源:2007年普通高等学校招生全国统一考试理科数学卷(海南) 题型:解答题
(本小题满分12分)
如图,面积为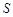 的正方形
的正方形 中有一个不规则的图形M,可按下面方法估计M的面积:在正方形
中有一个不规则的图形M,可按下面方法估计M的面积:在正方形 中随机投掷
中随机投掷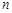 个点,若
个点,若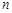 个点中有
个点中有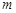 个点落入M中,则M的面积的估计值为
个点落入M中,则M的面积的估计值为 . 假设正方形
. 假设正方形 的边长为2,M的面积为1,并向正方形
的边长为2,M的面积为1,并向正方形 中随机投掷10 000个点,以
中随机投掷10 000个点,以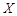 表示落入M中的点的数目.
表示落入M中的点的数目.
(Ⅰ)求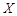 的均值
的均值 ;
;
 (Ⅱ)求用以上方法估计M的面积时,M的面积的估计值与实际值之差在区间
(Ⅱ)求用以上方法估计M的面积时,M的面积的估计值与实际值之差在区间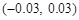 内的概率.
内的概率.
附表:
|
|
2424 |
2425 |
2574 |
2575 |
|
|
0.0403 |
0.0423 |
0.9570 |
0.9590 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com