
【题目】记![]() 表示正整数
表示正整数![]() 在十进制下的各位数码之和.定义
在十进制下的各位数码之和.定义![]() ,证明:对任意的
,证明:对任意的![]() ,存在无穷多个
,存在无穷多个![]() ,
,![]() ,使得
,使得![]() .
.
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 与二次曲线
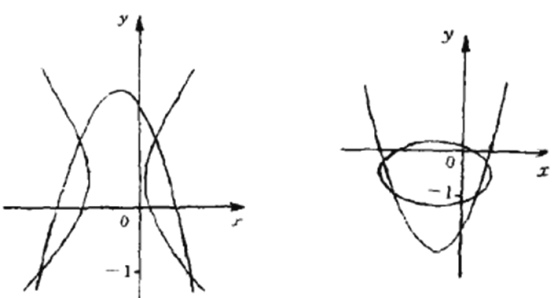
与二次曲线![]() 有4个不同的交点,由下面的草图可以看出,下面三个结论是成立的,请给出证明.
有4个不同的交点,由下面的草图可以看出,下面三个结论是成立的,请给出证明.
(1).两曲线的4个交点中,至少有两个交点位于![]() 轴的下方;
轴的下方;
(2).抛物线![]() 必与
必与![]() 轴有两个不同的交点,记为
轴有两个不同的交点,记为![]() ,
,![]() ,
,![]() ;
;
(3).两曲线的4个交点中,必存在一点![]() ,使
,使![]() .
.
注.对![]() 、
、![]() 、
、![]() 的不同取值会有无数个图形,此处仅就
的不同取值会有无数个图形,此处仅就![]() ,
,![]() 各给出一个示意图,同时也就限制“由图看出”的解答.
各给出一个示意图,同时也就限制“由图看出”的解答.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从1到9的九个数字中取三个偶数四个奇数,试问:
①能组成多少个没有重复数字的七位数?
②上述七位数中三个偶数排在一起的有几个?
③在①中的七位数中,偶数排在一起、奇数也排在一起的有几个?
④在①中任意两偶数都不相邻的七位数有几个?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线y2=2px的焦点为F,准线方程是x=﹣1.
(I)求此抛物线的方程;
(Ⅱ)设点M在此抛物线上,且|MF|=3,若O为坐标原点,求△OFM的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司招聘员工,先由两位专家面试,若两位专家都同意通过,则视作通过初审予以录用;若这两位专家都未同意通过,则视作未通过初审不予录用;当这两位专家意见不一致时,再由第三位专家进行复审,若能通过复审则予以录用,否则不予录用.设应聘人员获得每位初审专家通过的概率均为![]() ,复审能通过的概率为
,复审能通过的概率为![]() ,各专家评审的结果相互独立.
,各专家评审的结果相互独立.
(1)求某应聘人员被录用的概率;
(2)若4人应聘,设X为被录用的人数,试求随机变量X的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的选项为( )
①平面外一条直线与平面内的一条直线平行,则该直线与此平面平行;
②一个平面内的一条直线与另一个平面平行,则这两个平面平行;
③一条直线与一个平面内的两条直线垂直,则该直线与此平面垂直;
④一个平面过另一个平面的垂线,则这两个平面垂直.
A.①②B.②③C.①④D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 、
、![]() 为平面上两个点集,满足
为平面上两个点集,满足![]() ,
,![]() ,且任意三点不共线.在集合
,且任意三点不共线.在集合![]() 和
和![]() 间各连若干条线段,每条线段均一个端点在集合
间各连若干条线段,每条线段均一个端点在集合![]() 中,另一个端点在集合
中,另一个端点在集合![]() 中,且任意两点间至多连一条线段,记所有线段构成的集合为
中,且任意两点间至多连一条线段,记所有线段构成的集合为![]() .若集合
.若集合![]() 满足对于集合
满足对于集合![]() 或
或![]() 中任意一点均至少连出
中任意一点均至少连出![]() 条线段,则称集合
条线段,则称集合![]() 是“
是“![]() 一好的”.试确定
一好的”.试确定![]() 的最大值,使得去掉任意一条线段,集合
的最大值,使得去掉任意一条线段,集合![]() 均不是
均不是![]() 一好的.
一好的.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com