
【题目】已知![]() 为实数,函数
为实数,函数![]() .
.
(1)若![]() 是函数
是函数![]() 的一个极值点,求实数
的一个极值点,求实数![]() 的取值;
的取值;
(2)设![]() ,若
,若![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1) ![]() ,(2)
,(2) ![]() .
.
【解析】试题分析:(1)求出函数f(x)定义域,函数的导函数f′(x),假设存在实数a,使f(x)在x=3处取极值,则f′(3)=0,求出a,验证推出结果.
(2)由f (x0)≤g(x0) 得:(x0﹣lnx0)a≥x02﹣2x0,记F(x)=x﹣lnx(x>0),求出F′(x),推出F(x)≥F(1)=1>0,转化a≥![]() ,记G(x)=
,记G(x)=![]() ,x∈[
,x∈[![]() ,e]求出导函数,求出最大值,列出不等式求解即可.
,e]求出导函数,求出最大值,列出不等式求解即可.
解析:(1)函数![]() 定义域为
定义域为![]() ,
,
![]() .
.
∵![]() 是函数
是函数![]() 的一个极值点,∴
的一个极值点,∴![]() ,解得
,解得![]() .
.
经检验![]() 时,
时, ![]() 是函数
是函数![]() 的一个极小值点,符合题意,
的一个极小值点,符合题意,
∴![]() .
.
(2)由![]() ,得
,得![]() ,
,
记![]() ,
,
∴![]() ,
,
∴当![]() 时,
时, ![]() ,
, ![]() 单调递减;
单调递减;
当![]() 时,
时, ![]() ,
, ![]() 单调递増.
单调递増.
∴![]() ,
,
∴![]() ,记
,记![]() ,
,
∴
 .
.
∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() 时,
时, ![]() ,
, ![]() 单调递减;
单调递减;
![]() 时,
时, ![]() ,
, ![]() 单调递增,
单调递增,
∴![]() ,
,
∴![]() .
.
故实数![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】设函数f(x)=ax﹣(k﹣1)a﹣x(a>0且a≠1)是定义域为R的奇函数.
(1)求k值;
(2)若f(1)<0,试判断y=f(x)的单调性并求使不等式f(x2+tx)+f(4﹣x)<0恒成立的t的取值范围;
(3)若f(1)= ![]() ,g(x)=a2x+a﹣2x﹣2f(x),求k∈N+在[1,+∞)上的最小值.
,g(x)=a2x+a﹣2x﹣2f(x),求k∈N+在[1,+∞)上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别为内角A,B,C的对边,且asinB=﹣bsin(A+ ![]() ).
).
(1)求A;
(2)若△ABC的面积S= ![]() c2 , 求sinC的值.
c2 , 求sinC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x﹣1|+|2x+a|,g(x)=x+3.
(1)当a=﹣2时,求不等式f(x)<g(x)的解集;
(2)设a>﹣1,且当x∈(﹣ ![]() ,
, ![]() )时,f(x)≤g(x),求a的取值范围.
)时,f(x)≤g(x),求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某批发市场对某种商品的日销售量(单位:吨)进行统计,最近50天的统计结果如下:
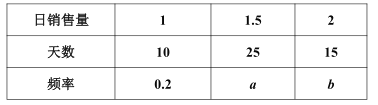
若以上表中频率作为概率,且每天的销售量相互独立.
(1)求5天中该种商品恰好有两天的日销售量为1.5吨的概率;
(2)已知每吨该商品的销售利润为2千元, ![]() 表示该种商品某两天销售利润的和(单位:千元),求
表示该种商品某两天销售利润的和(单位:千元),求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知离散型随机变量X的分布列如表:
X | ﹣1 | 0 | 1 | 2 |
P | a | b | c |
|
若E(X)=0,D(X)=1,则a,b的值分别为( )
A.![]() ,
, ![]()
B.![]() ,
, ![]()
C.![]() ,
, ![]()
D.![]() ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
已知函数f(x)=x3+ax2+bx+c,曲线y=f(x)在点x=1处的切线方程为
l:y=3x+1,且当x=![]() 时,y=f(x)有极值.
时,y=f(x)有极值.
(1)求a,b,c的值;
(2)求y=f(x)在[-3,1]上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“莞马”活动中的α机器人一度成为新闻热点,为检测其质量,从一生产流水线上抽取20件该产品,其中合格产品有15件,不合格的产品有5件.
(1)现从这20件产品中任意抽取2件,记不合格的产品数为X,求X的分布列及数学期望;
(2)用频率估计概率,现从流水线中任意抽取三个机器人,记ξ为合格机器人与不合格机器人的件数差的绝对值,求ξ的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com