
【题目】如图所示,我国某海岸线可看作由圆弧AB和射线BC连接而成,其中圆弧AB所在圆O的半径为12海里,圆心角为120°,规定外轮除特许外,不得进入离我国海岸线12海里以内的区域.在港口A处设有观察站,外轮一旦进入规定区域,观察站会接收到预警信号,现从A处测得一外轮在北偏东60°,距离港口x海里的P处,沿直线PA方向航行.
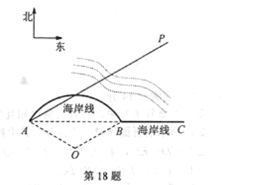
(1)当x=30时,分别求出外轮到海岸线BC和弧AB的最短距离,并判断观察站是否接收到预警信号?
(2)当x为何值时,观察站开始接收到预警信号?
科目:高中数学 来源: 题型:
【题目】下面几种推理过程是演绎推理的是( )
A. 某校高三有8个班,1班有51人,2班有53人,3班有52人,由此推测各班人数都超过50人
B. 由三角形的性质,推测空间四面体的性质
C. 平行四边形的对角线互相平分,菱形是平行四边形,所以菱形的对角线互相平分
D. 在数列![]() 中,
中,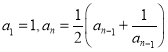 ,可得
,可得![]() ,由此归纳出
,由此归纳出![]() 的通项公式
的通项公式![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() 是两条不同的直线,
是两条不同的直线,![]() ,
,![]() ,
,![]() 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题:
①若![]() ,
,![]() ,则
,则![]()
②若![]() ,
,![]() ,
,![]() ,则
,则![]()
③若![]() ,
,![]() ,则
,则![]()
④若![]() ,
,![]() ,则
,则![]()
其中正确命题的序号是( )
A.①和②B.②和③C.③和④D.①和④
查看答案和解析>>
科目:高中数学 来源: 题型:
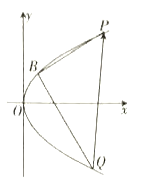
【题目】已知点![]() 是抛物线
是抛物线![]() 上一点,
上一点,![]() 为
为![]() 的焦点.
的焦点.
(1)若![]() ,
,![]() 是
是![]() 上的两点,证明:
上的两点,证明:![]() ,
,![]() ,
,![]() 依次成等比数列.
依次成等比数列.
(2)过![]() 作两条互相垂直的直线与
作两条互相垂直的直线与![]() 的另一个交点分别交于
的另一个交点分别交于![]() ,
,![]() (
(![]() 在
在![]() 的上方),求向量
的上方),求向量![]() 在
在![]() 轴正方向上的投影的取值范围.
轴正方向上的投影的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一位幼儿园老师给班上k(k≥3)个小朋友分糖果.她发现糖果盒中原有糖果数为a0,就先从别处抓2块糖加入盒中,然后把盒内糖果的![]() 分给第一个小朋友;再从别处抓2块糖加入盒中,然后把盒内糖果的
分给第一个小朋友;再从别处抓2块糖加入盒中,然后把盒内糖果的![]() 分给第二个小朋友;…,以后她总是在分给一个小朋友后,就从别处抓2块糖放入盒中,然后把盒内糖果的
分给第二个小朋友;…,以后她总是在分给一个小朋友后,就从别处抓2块糖放入盒中,然后把盒内糖果的![]() 分给第n(n=1,2,3,…k)个小朋友.如果设分给第n个小朋友后(未加入2块糖果前)盒内剩下的糖果数为an.
分给第n(n=1,2,3,…k)个小朋友.如果设分给第n个小朋友后(未加入2块糖果前)盒内剩下的糖果数为an.
(1)当k=3,a0=12时,分别求a1,a2,a3;
(2)请用an-1表示an;令bn=(n+1)an,求数列{bn}的通项公式;
(3)是否存在正整数k(k≥3)和非负整数a0,使得数列{an}(n≤k)成等差数列,如果存在,请求出所有的k和a0,如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com