
【题目】已知函数f(x)=x|2a﹣x|+2x,a∈R.
(1)若a=0,判断函数y=f(x)的奇偶性,并加以证明;
(2)若函数f(x)在R上是增函数,求实数a的取值范围;
(3)若存在实数a∈[﹣2,2],使得关于x的方程f(x)﹣tf(2a)=0有三个不相等的实数根,求实数t的取值范围.
【答案】
(1)解:函数y=f(x)为奇函数.
理由:当a=0时,f(x)=x|x|+2x,
f(﹣x)=﹣x|x|﹣2x=﹣f(x),
∴函数y=f(x)为奇函数
(2)解:f(x)= 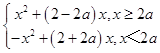 ,
,
当x≥2a时,f(x)的对称轴为:x=a﹣1;
当x<2a时,y=f(x)的对称轴为:x=a+1;
∴当a﹣1≤2a≤a+1时,f(x)在R上是增函数,
即﹣1≤a≤1时,函数f(x)在R上是增函数
(3)解:方程f(x)﹣tf(2a)=0的解即为方程f(x)=tf(2a)的解.
①当﹣1≤a≤1时,函数f(x)在R上是增函数,
∴关于x的方程f(x)=tf(2a)不可能有三个不相等的实数根;
②当a>1时,即2a>a+1>a﹣1,
∴f(x)在(﹣∞,a+1)上单调增,
在(a+1,2a)上单调减,在(2a,+∞)上单调增,
∴当f(2a)<tf(2a)<f(a+1)时,
关于x的方程f(x)=tf(2a)有三个不相等的实数根;
即4a<t4a<(a+1)2,
∵a>1,
∴1<t< ![]() (a+
(a+ ![]() +2).
+2).
设h(a)= ![]() (a+
(a+ ![]() +2),
+2),
∵存在a∈[﹣2,2],
使得关于x的方程f(x)=tf(2a)有三个不相等的实数根,
∴1<t<h(a)max,
又可证h(a)= ![]() (a+
(a+ ![]() +2)在(1,2]上单调增,
+2)在(1,2]上单调增,
∴<h(a)max= ![]() ,
,
∴1<t< ![]() ,
,
③当a<﹣1时,即2a<a﹣1<a+1,
∴f(x)在(﹣∞,2a)上单调增,
在(2a,a﹣1)上单调减,在(a﹣1,+∞)上单调增,
∴当f(a﹣1)<tf(2a)<f(2a)时,
关于x的方程f(x)=tf(2a)有三个不相等的实数根;
即﹣(a﹣1)2<t4a<4a,
∵a<﹣1,
∴1<t<﹣ ![]() (a+
(a+ ![]() ﹣2),
﹣2),
设g(a)=﹣ ![]() (a+
(a+ ![]() ﹣2),
﹣2),
∵存在a∈[﹣2,2],使得关于x的方程f(x)=tf(2a)有三个不相等的实数根,
∴1<t<g(a)max,
又可证g(a)=﹣ ![]() (a+
(a+ ![]() ﹣2)在[﹣2,﹣1)上单调减,
﹣2)在[﹣2,﹣1)上单调减,
∴g(a)max= ![]() ,
,
∴1<t< ![]() ;
;
综上:1<t< ![]() .
.
【解析】(1)若a=0,根据函数奇偶性的定义即可判断函数y=f(x)的奇偶性;(2)根据函数单调性的定义和性质,利用二次函数的性质即可求实数a的取值范围;(3)根据方程有三个不同的实数根,建立条件关系即可得到结论.
【考点精析】解答此题的关键在于理解奇偶性与单调性的综合的相关知识,掌握奇函数在关于原点对称的区间上有相同的单调性;偶函数在关于原点对称的区间上有相反的单调性.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:
【题目】某百货公司1~6月份的销售量x与利润y的统计数据如表:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
销售量x(万件) | 10 | 11 | 13 | 12 | 8 | 6 |
利润y(万元) | 22 | 25 | 29 | 26 | 16 | 12 |
(参考公式: ![]() =
= 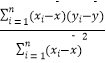 )=
)= 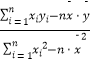 ,
, ![]() .
.
(1)根据2~5月份的统计数据,求出y关于x的回归直线方程 ![]() ;
;
(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差均不超过2万元,则认为得到的回归直线方程是理想的,试问所得回归直线方程是否理想?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)对任意实数x,y均有f(x)=f( ![]() )+f(
)+f( ![]() ).当x>0时,f(x)>0
).当x>0时,f(x)>0
(1)判断函数f(x)在R上的单调性并证明;
(2)设函数g(x)与函数f(x)的奇偶性相同,当x≥0时,g(x)=|x﹣m|﹣m(m>0),若对任意x∈R,不等式g(x﹣1)≤g(x)恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)= ![]() ﹣
﹣ ![]() ,若规定<x>表示不小于x的最小整数,则函数y=<f(x)>的值域是( )
,若规定<x>表示不小于x的最小整数,则函数y=<f(x)>的值域是( )
A.{0,1}
B.{0,﹣1}
C.{﹣1,1}
D.{﹣1,0,1}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,点A,B是单位圆O上的两点,A,B点分别在第一,而象限,点C是圆O与x轴正半轴的交点,若∠COA=60°,∠AOB=α,点B的坐标为(﹣ ![]() ,
, ![]() ).
). 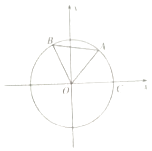
(1)求sinα的值;
(2)已知动点P沿圆弧从C点到A点匀速运动需要2秒钟,求动点P从A点开始逆时针方向作圆周运动时,点P的纵坐标y关于时间t(秒)的函数关系式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=ln ![]() ,则f(x)是( )
,则f(x)是( )
A.奇函数,且在(0,+∞)上单调递减
B.奇函数,且在(0,+∞)上单凋递增
C.偶函数,且在(0,+∞)上单调递减
D.偶函数,且在(0,+∞)上单凋递增
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π),在同一周期内,当x= ![]() 时,f(x)取得最大值3,当x=﹣
时,f(x)取得最大值3,当x=﹣ ![]() 时,f(x)取得最小值﹣3. (Ⅰ)求函数f(x)的解析式;
时,f(x)取得最小值﹣3. (Ⅰ)求函数f(x)的解析式;
(Ⅱ)求函数f(x)的单调递减区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com