
【题目】下列命题中错误的是
A. 若命题p为真命题,命题q为假命题,则命题“pV(q)”为真命题
B. 命题“若a+b≠7,则a≠2或b≠5”为真命题
C. 命题“若x2-x=0,则x=0或x=1”的否命题为“若x2-x=0,则x≠0且x≠1”
D. 命题p: ![]() x>0,sinx>2x-1,则
x>0,sinx>2x-1,则![]() p为
p为![]() x>0,sinx≤2x-1
x>0,sinx≤2x-1
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
在直角坐标系xOy中,设倾斜角为α的直线l:![]() (t为参数)与曲线C:
(t为参数)与曲线C:![]() (θ为参数)相交于不同的两点A,B.
(θ为参数)相交于不同的两点A,B.
(Ⅰ)若α=![]() ,求线段AB中点M的坐标;
,求线段AB中点M的坐标;
(Ⅱ)若|PA|·|PB|=|OP|![]() ,其中P(2,
,其中P(2,![]() ),求直线l的斜率.
),求直线l的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax﹣cosx,a≠0.
(1)若函数f(x)为单调函数,求a的取值范围;
(2)若x∈[0,2π],求:当a≥![]() 时,函数f(x)仅有一个零点.
时,函数f(x)仅有一个零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}为等差数列,前n项和为Sn(n∈N*),{bn}是首项为2的等比数列,且公比大于0,b2+b3=12,b3=a4-2a1,S11=11b4.
(1)求{an}和{bn}的通项公式;
(2)求数列{a2nbn}的前n项和(n∈N*).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,
中,
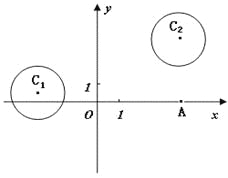
已知圆![]() 和圆
和圆![]() .
.
(1)若直线![]() 过点
过点![]() ,且被圆
,且被圆![]() 截得的弦长为
截得的弦长为![]() ,
,
求直线![]() 的方程;(2)设P为平面上的点,满足:
的方程;(2)设P为平面上的点,满足:
存在过点P的无穷多对互相垂直的直线![]() 和
和![]() ,
,
它们分别与圆![]() 和圆
和圆![]() 相交,且直线
相交,且直线![]() 被圆
被圆![]()
截得的弦长与直线![]() 被圆
被圆![]() 截得的弦长相等,试求所有满足条件的点P的坐标。
截得的弦长相等,试求所有满足条件的点P的坐标。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,椭圆
,椭圆![]() 的长轴长为4.
的长轴长为4.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,是否存在实数
两点,是否存在实数![]() 使得以线段
使得以线段![]() 为直径的圆恰好经过坐标原点
为直径的圆恰好经过坐标原点![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为弘扬中华民族传统文化,某中学学生会对本校高一年级1000名学生课余时间参加传统文化活动的情况,随机抽取50名学生进行调查,将数据分组整理后,列表如下:
参加场数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
参加人数占调查人数的百分比 | 8% | 10% | 20% | 26% | 18% | 12% | 4% | 2% |
估计该校高一学生参加传统文化活动情况正确的是().
A. 参加活动次数是3场的学生约为360人B. 参加活动次数是2场或4场的学生约为480人
C. 参加活动次数不高于2场的学生约为280人D. 参加活动次数不低于4场的学生约为360人
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区随着经济的发展,居民收入逐年增长,银行储蓄连年增长,下表是该地区某银行连续五年的储蓄存款(年底结算):
年份 |
|
|
|
|
|
储蓄存款 |
|
|
|
|
|
为方便研究,工作人员对上表的数据做了如下处理:![]() ,
,![]() 得到下表:
得到下表:
|
|
|
|
|
|
|
|
|
|
|
|
(1)用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)通过(1)中的方程,求出![]() 关于
关于![]() 的线性回归方程,并用所求回归方程预测
的线性回归方程,并用所求回归方程预测![]() 年底,该地储蓄存款额可达多少?
年底,该地储蓄存款额可达多少?
(附:参考公式![]() ,其中
,其中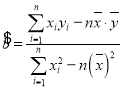 ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com