
【题目】抛物线C1: ![]() 的焦点与双曲线C2:
的焦点与双曲线C2: ![]() 的右焦点的连线交C1于第一象限的点M.若C1在点M处的切线平行于C2的一条渐近线,则p=( )
的右焦点的连线交C1于第一象限的点M.若C1在点M处的切线平行于C2的一条渐近线,则p=( )
A.![]()
B.![]()
C.![]()
D.![]()
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:
【题目】如图1,已知四边形BCDE为直角梯形,![]() ,
,![]() ,且
,且![]() ,A为BE的中点
,A为BE的中点![]() 将
将![]() 沿AD折到
沿AD折到![]() 位置
位置![]() 如图
如图![]() ,连结PC,PB构成一个四棱锥
,连结PC,PB构成一个四棱锥![]() .
.

![]() Ⅰ
Ⅰ![]() 求证
求证![]() ;
;
![]() Ⅱ
Ⅱ![]() 若
若![]() 平面ABCD.
平面ABCD.
![]() 求二面角
求二面角![]() 的大小;
的大小;
![]() 在棱PC上存在点M,满足
在棱PC上存在点M,满足![]() ,使得直线AM与平面PBC所成的角为
,使得直线AM与平面PBC所成的角为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《张邱建算经》是中国古代数学史上的杰作,该书中有首古民谣记载了一数列问题:“南山一棵竹,竹尾风割断,剩下三十节,一节一个圈,头节高五寸①,头圈一尺三②,逐节多三分③,逐圈少分三④,一蚁往上爬,遇圈则绕圈。爬到竹子顶,行程是多远?”(注释:①第节的高度为0.5尺;②第一圈的周长为1.3尺;③每节比其下面的一节多0.03尺;④每圈周长比其下面的一圈少0.013尺),问:此民谣提出的问题的答案是( )
A. 61.395尺B. 61.905尺C. 72.705尺D. 73.995尺
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】先阅读下列题目的证法,再解决后面的问题.
已知a1,a2∈R,且a1+a2=1,求证:a+a≥![]() .
.
证明:构造函数f(x)=(x-a1)2+(x-a2)2,则f(x)=2x2-2(a1+a2)x+a+a=2x2-2x+a+a.
因为对一切x∈R,恒有f(x)≥0,
所以Δ=4-8(a+a)≤0,从而得a+a≥![]() .
.
(1)若a1,a2,…,an∈R,a1+a2+…+an=1,请由上述结论写出关于a1,a2,…,an的推广式;
(2)参考上述证法,请对你推广的结论加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】ΔABC的内角A,B,C的对边分别为a,b,c,根据下列条件解三角形,其中有两解的是
A. a=2,b=3,A=30°B. b=6,c=4,A=120°
C. a=4![]() ,b=6,A=60°D. a=3,b=6,A=30°
,b=6,A=60°D. a=3,b=6,A=30°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆C: ![]() 的左右焦点分别是F1 , F2 , 离心率为
的左右焦点分别是F1 , F2 , 离心率为 ![]() ,过F1且垂直于x轴的直线被椭圆C截得的线段长为1.
,过F1且垂直于x轴的直线被椭圆C截得的线段长为1.
(1)求椭圆C的方程;
(2)点P是椭圆C上除长轴端点外的任一点,连接PF1 , PF2 , 设∠F1PF2的角平分线PM交C的长轴于点M(m,0),求m的取值范围;
(3)在(2)的条件下,过点P作斜率为k的直线l,使得l与椭圆C有且只有一个公共点,设直线PF1 , PF2的斜率分别为k1 , k2 , 若k≠0,试证明 ![]() 为定值,并求出这个定值.
为定值,并求出这个定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中以O为极点,x轴正半轴为极轴建立坐标系.圆C1 , 直线C2的极坐标方程分别为ρ=4sinθ,ρcos( ![]() )=2
)=2 ![]() .
.
(1)求C1与C2交点的极坐标;
(2)设P为C1的圆心,Q为C1与C2交点连线的中点,已知直线PQ的参数方程为 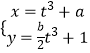 (t∈R为参数),求a,b的值.
(t∈R为参数),求a,b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com