
【题目】已知项数为![]() 的数列
的数列![]() 满足如下条件:①
满足如下条件:①![]() ;②
;②![]() 若数列
若数列![]() 满足
满足![]() 其中
其中![]() 则称
则称![]() 为
为![]() 的“伴随数列”.
的“伴随数列”.
(I)数列![]() 是否存在“伴随数列”,若存在,写出其“伴随数列”;若不存在,请说明理由;
是否存在“伴随数列”,若存在,写出其“伴随数列”;若不存在,请说明理由;
(II)若![]() 为
为![]() 的“伴随数列”,证明:
的“伴随数列”,证明:![]() ;
;
(III)已知数列![]() 存在“伴随数列”
存在“伴随数列”![]() 且
且![]() 求
求![]() 的最大值.
的最大值.
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 上一点
上一点![]() 到焦点的距离为
到焦点的距离为![]() ,过
,过![]() 作两条互相垂直的直线
作两条互相垂直的直线![]() 和
和![]() ,其中斜率为
,其中斜率为![]()
![]() 与抛物线交于A,B,
与抛物线交于A,B,![]() 与y轴交于C,点Q满足:
与y轴交于C,点Q满足:![]()
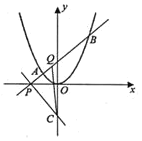
(1)求抛物线的方程;
(2)求三角形PQC面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,求实数
,求实数![]() 的值;
的值;
(2)证明:当![]() 时,
时,![]() 在
在![]() 上有两个极值点;
上有两个极值点;
(3)设![]() ,若
,若![]() 在
在![]() 上是单调减函数(
上是单调减函数(![]() 为自然对数的底数),求实数
为自然对数的底数),求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点为极点,x轴的非负半轴为极轴,建立极坐标系,并在两种坐标系中取相同的长度单位,已知直线l的参数方程为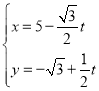 (t为参数),圆C的极坐标方程为
(t为参数),圆C的极坐标方程为![]()
(1)求直线l和圆C的直角坐标方程;
(2)若点![]() 在圆C上,求
在圆C上,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右顶点为A,上顶点为B,O为坐标原原点,点O到直线AB的距离为
的右顶点为A,上顶点为B,O为坐标原原点,点O到直线AB的距离为![]() ,
,![]() 的面积为1.
的面积为1.
(1)求榷圆的标准方程;
(2)直线![]() 与椭圆交于C,D两点,若直线
与椭圆交于C,D两点,若直线![]() 直线AB,设直线AC,BD的斜率分别为
直线AB,设直线AC,BD的斜率分别为![]() 证明:
证明:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某民航部门统计的2019年春运期间12个城市售出的往返机票的平均价格以及相比上年同期变化幅度的数据统计图表如图所示,根据图表,下面叙述不正确的是( )
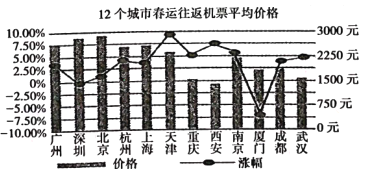
A. 同去年相比,深圳的变化幅度最小且厦门的平均价格有所上升
B. 天津的平均价格同去年相比涨幅最大且2019年北京的平均价格最高
C. 2019年平均价格从高到低居于前三位的城市为北京、深圳、广州
D. 同去年相比,平均价格的涨幅从高到低居于前三位的城市为天津、西安、南京
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司年会有幸运抽奖环节,一个箱子里有相同的十个兵乓球,球上分别标0,1,2,…,9这十个自然数,每位员工有放回的依次取出三个球.规定:每次取出的球所标数字不小于后面取出的球所标数字即中奖.中奖奖项:三个数字全部相同中一等奖,奖励10000元现金;三个数字中有两个数字相同中二等奖,奖励5000元现金;三个数字各不相同中三等奖,奖励2000元现金;其它不中奖,没有奖金.
(1)求员工A中二等奖的概率;
(2)设员工A中奖奖金为X,求X的分布列;
(3)员工B是优秀员工,有两次抽奖机会,求员工B中奖奖金的期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】全民参与是打赢新型冠状病毒防疫战的根本方法.在防控疫情的过程中,某小区的“卡口”工作人员由“社区工作者”“下沉干部”“志愿者”三种身份的人员构成,其中社区工作者3人,下沉干部2人,志愿者1人.某电视台某天上午随机抽取2人进行访谈,某报社在该天下午随机抽取1人进行访谈.
(1)设![]() 表示上午抽到的社区工作者的人数,求随机变量
表示上午抽到的社区工作者的人数,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(2)设![]() 为事件“全天抽到的
为事件“全天抽到的![]() 名工作人员的身份互不相同”,求事件
名工作人员的身份互不相同”,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com