
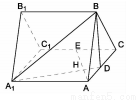
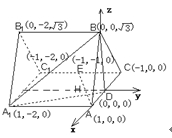
如图,正三棱柱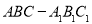 所有棱长都是2,D棱AC的中点,E是
所有棱长都是2,D棱AC的中点,E是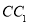 棱的中点,AE交
棱的中点,AE交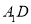 于点H.
于点H.
(1)求证: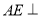 平面
平面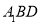 ;
;
(2)求二面角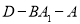 的余弦值;
的余弦值;
(3)求点 到平面
到平面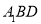 的距离.
的距离.
(1)参考解析;(2) 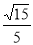 ;(3)
;(3) 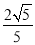
【解析】
试题分析:(1)由正三棱柱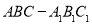 ,可得平面ACB⊥平面
,可得平面ACB⊥平面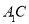 .又DB⊥AC.所以如图建立空间直角坐标系.分别点A,E,B,D,
.又DB⊥AC.所以如图建立空间直角坐标系.分别点A,E,B,D, 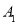 的坐标,得出相应的向量.即可得到向量AE与向量BD,向量
的坐标,得出相应的向量.即可得到向量AE与向量BD,向量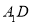 的数量积为零.即可得直线
的数量积为零.即可得直线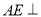 平面
平面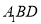 .
.
(2)由平面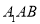 ,平面
,平面 分别求出这两个平面的法向量,根据法向量的夹角得到二面角
分别求出这两个平面的法向量,根据法向量的夹角得到二面角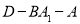 的余弦值(根据图形取锐角).
的余弦值(根据图形取锐角).
(3)点到平面的距离,转化为直线与法向量的关系,再通过解三角形的知识即可得点到平面的距离.本小题关键是应用解三角形的知识.
试题解析:(1)证明:建立如图所示, 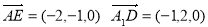
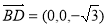 ∵
∵
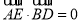
∴ 即AE⊥A1D, AE⊥BD
即AE⊥A1D, AE⊥BD
∴AE⊥面A1BD
(2)由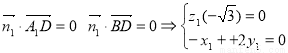 ∴取
∴取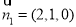
设面AA1B的法向量为 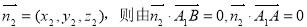
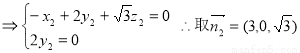 ,
, 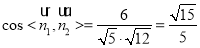
由图可知二面角D—BA1—A的余弦值为 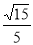
(3)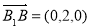 ,平面A1BD的法向量取
,平面A1BD的法向量取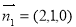
则B1到平面A1BD的距离d=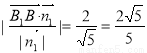
考点:1.空间坐标系的建立.2.线面垂直的证明.4.二面角的求法.5.点到平面的距离公式.


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源:2013-2014学年江西省南昌市高三第二次模拟考试理科数学试卷(解析版) 题型:选择题
已知函数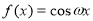
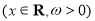 的最小正周期为
的最小正周期为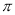 ,为了得到函数
,为了得到函数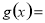
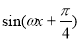 的图象,只要将
的图象,只要将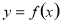 的图象( )
的图象( )
A.向左平移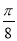 个单位长度 B.向右平移
个单位长度 B.向右平移 个单位长度
个单位长度
C.向左平移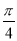 个单位长度 D.向右平移
个单位长度 D.向右平移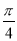 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省高三联合考试理科数学试卷(解析版) 题型:选择题
已知数列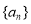 ,若点
,若点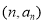
 均在直线
均在直线 上,则数列
上,则数列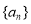 的前9项和
的前9项和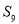 等于( )
等于( )
A.18 B.20 C.22 D.24
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省高三联合考试文科数学试卷(解析版) 题型:选择题
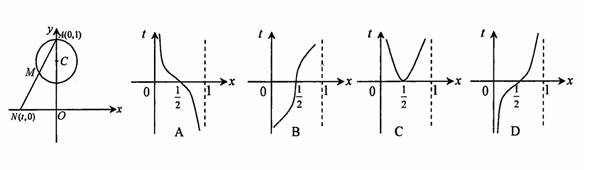
如图,把周长为1的圆的圆心C放在y轴上,顶点A(0,1),一动点M从A开始逆时针绕圆运动一周,记弧AM=x,直线AM与x轴交于点N(t,0),则函数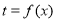 的图像大致为( )
的图像大致为( )
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省高三联合考试文科数学试卷(解析版) 题型:选择题
月底,某商场想通过抽取发票的10%来估计该月的销售额,先将该月的全部销售发票存根进行了编号:1,2,3,…,然后拟采用系统抽样的方法获取一个样本.若从编号为1,2,…,10的前10张发票存根中随机抽取一张,然后再按系统抽样的方法依编号逐次产生第二张、第三张、第四张、…,则抽样中产生的第二张已编号的发票存根,其编号不可能是( )
A.19 B.17 C.23 D.13
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省上饶市高三第二次模拟考试理科数学试卷(解析版) 题型:填空题
(坐标系与参数方程选做题)在极坐标系中,曲线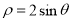 与
与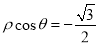 的交点的极坐标为_________.
的交点的极坐标为_________.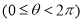
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省上饶市高三第二次模拟考试理科数学试卷(解析版) 题型:选择题
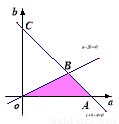
设点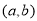 是区域
是区域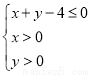 内的随机点,函数
内的随机点,函数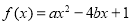 在区间
在区间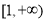 上是增函数的概率为 ( )
上是增函数的概率为 ( )
A. 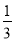 B.
B. 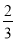 C.
C. 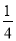 D.
D. 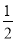
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省连云港市高三3月第二次调研考试理科数学试卷(解析版) 题型:解答题
如图,在平面直角坐标系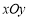 中,已知
中,已知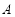 ,
,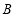 ,
,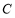 是椭圆
是椭圆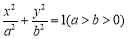 上不同的三点,
上不同的三点,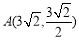 ,
,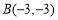 ,
,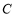 在第三象限,线段
在第三象限,线段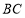 的中点在直线
的中点在直线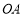 上.
上.
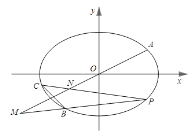
(1)求椭圆的标准方程;
(2)求点C的坐标;
(3)设动点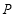 在椭圆上(异于点
在椭圆上(异于点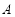 ,
,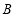 ,
,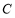 )且直线PB,PC分别交直线OA于
)且直线PB,PC分别交直线OA于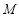 ,
,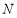 两点,证明
两点,证明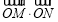 为定值并求出该定值.
为定值并求出该定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com