
分析 (Ⅰ)利用直线垂直的性质求解;(Ⅱ)利用直线平行的性质求解即可.
解答 解:(Ⅰ)直线l1:2x-y+1=0,l2:ax+4y-2=0,
若l1⊥l2,则2a-4=0,解得:a=2;
(Ⅱ)若l1∥l2,则$\frac{a}{2}$=$\frac{4}{-1}$≠$\frac{-2}{1}$,
解得:a=-8,
∴l2:2x-y+$\frac{1}{2}$=0,
∴d=$\frac{|1-\frac{1}{2}|}{\sqrt{{2}^{2}{+1}^{2}}}$=$\frac{\sqrt{5}}{10}$.
点评 本题考查实数值的求法,考查直线的位置关系,是基础题,解题时要认真审题,注意直线平行的性质的灵活运.


 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案科目:高中数学 来源: 题型:解答题
| x | 2 | 3 | 4 | 5 | 6 |
| y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2,3] | B. | (-∞,2]∪[3,+∞) | C. | [-1,6] | D. | [-6,1] |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年内蒙古高二文上月考一数学试卷(解析版) 题型:选择题
若P是以F1,F2为焦点的椭圆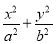 =1(a>b>0)上的一点,且
=1(a>b>0)上的一点,且 =0,tan∠PF1F2=
=0,tan∠PF1F2=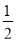 ,则此椭圆的离心率为( )
,则此椭圆的离心率为( )
A.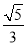 B.
B.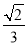 C.
C.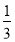 D.
D.
查看答案和解析>>
科目:高中数学 来源:2016-2017学年江西吉安一中高二上段考一数学(文)试卷(解析版) 题型:填空题
已知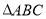 为等腰直角三角形,斜边
为等腰直角三角形,斜边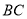 上的中线
上的中线 ,将
,将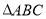 沿
沿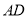 折成
折成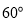 的二面角,连结
的二面角,连结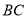 ,则三棱锥
,则三棱锥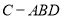 的体积为__________.
的体积为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com