
已知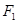 、
、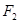 分别是椭圆
分别是椭圆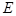 :
: 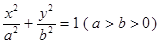 的左、右焦点,点
的左、右焦点,点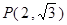 在直线
在直线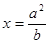 上,线段
上,线段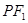 的垂直平分线经过点
的垂直平分线经过点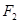 .直线
.直线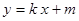 与椭圆
与椭圆 交于不同的两点
交于不同的两点 、
、 ,且椭圆
,且椭圆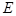 上存在点
上存在点 ,使
,使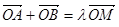 ,其中
,其中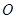 是坐标原点,
是坐标原点,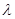 是实数.
是实数.
(Ⅰ)求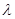 的取值范围;
的取值范围;
(Ⅱ)当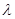 取何值时,
取何值时,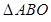 的面积最大?最大面积等于多少?
的面积最大?最大面积等于多少?
(Ⅰ)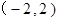 ;(Ⅱ)当
;(Ⅱ)当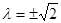 时,
时,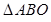 的面积最大,最大面积为
的面积最大,最大面积为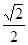 .
.
【解析】
试题分析:1.由于题目较长,一些考生不能识别有效信息,未能救出椭圆 的方程求.2. 第(Ⅰ)问,求
的方程求.2. 第(Ⅰ)问,求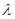 的取值范围.其主要步骤与方法为:由
的取值范围.其主要步骤与方法为:由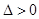 ,得关于
,得关于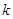 、
、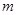 的不等式
的不等式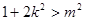 …… ①.由根与系数的关系、
…… ①.由根与系数的关系、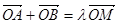 ,
,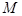 在椭圆
在椭圆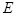 上,可以得到关于
上,可以得到关于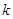 、
、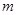 、
、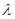 的等式
的等式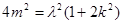 …… ②.把等式②代入①,可以达到消元的目的,但问题是这里一共有三个变量,就是消了
…… ②.把等式②代入①,可以达到消元的目的,但问题是这里一共有三个变量,就是消了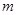 ,那还有关于
,那还有关于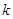 和
和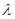 的不等式,如何求出
的不等式,如何求出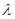 的取值范围呢?这将会成为难点.事实上,在把等式②代入①的过程中,
的取值范围呢?这将会成为难点.事实上,在把等式②代入①的过程中,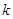 和
和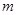 一起被消掉,得到了关于
一起被消掉,得到了关于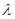 的不等式.解之即可.
的不等式.解之即可.
3.第(Ⅱ)问要把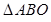 的面积函数先求出来.用弦长公式求底,用点到直线的距离公式求高,得到
的面积函数先求出来.用弦长公式求底,用点到直线的距离公式求高,得到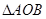 的面积
的面积
 ,函数中有两个自变量
,函数中有两个自变量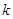 和
和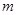 ,如何求函数的最大值呢?这又成为难点.这里很难想到把②代入面积函数中,因为②中含有三个变量,即使代入消掉一个后,面积函数依然有两个自变量.但这里很巧合的是:代入消掉
,如何求函数的最大值呢?这又成为难点.这里很难想到把②代入面积函数中,因为②中含有三个变量,即使代入消掉一个后,面积函数依然有两个自变量.但这里很巧合的是:代入消掉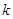 后,事实上,
后,事实上,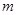 也自动地消除了,于是得到了面积
也自动地消除了,于是得到了面积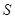 和自变量
和自变量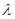 的函数关系
的函数关系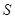
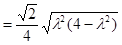 ,再由第(Ⅰ)中所得到的
,再由第(Ⅰ)中所得到的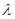 的取值范围
的取值范围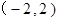 ,利用均值不等式,即可求出面积的最大值了.
,利用均值不等式,即可求出面积的最大值了.
试题解析::(Ⅰ)设椭圆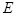 的半焦距为
的半焦距为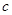 ,根据题意得
,根据题意得
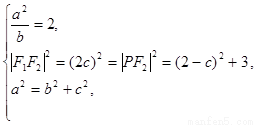 解方程组得
解方程组得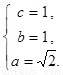
∴椭圆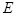 的方程为
的方程为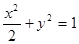 .
.
由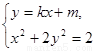 ,得
,得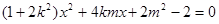 .
.
根据已知得关于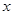 的方程
的方程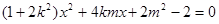 有两个不相等的实数根.
有两个不相等的实数根.
∴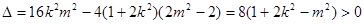 ,
,
化简得: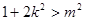 .
.
设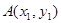 、
、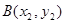 ,则
,则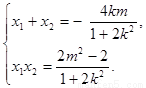
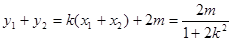 .
.
(1)当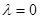 时,点
时,点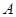 、
、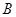 关于原点对称,
关于原点对称,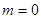 ,满足题意;
,满足题意;
(2)当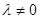 时,点
时,点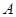 、
、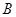 关于原点不对称,
关于原点不对称,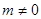 .
.
由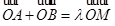 ,得
,得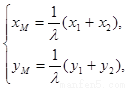 即
即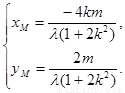
∵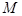 在椭圆
在椭圆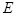 上,∴
上,∴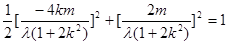 ,
,
化简得: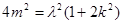 .
.
∵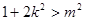 ,∴
,∴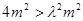 .
.
∵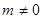 ,
,
∴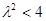 ,即
,即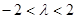 且
且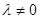 .
.
综合(1)、(2)两种情况,得实数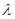 的取值范围是
的取值范围是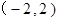 .
.
(Ⅱ)当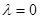 时,
时,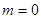 ,此时,
,此时,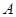 、
、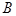 、
、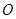 三点在一条直线上,不构成
三点在一条直线上,不构成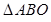 .
.
∴为使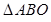 的面积最大,
的面积最大,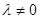 .
.
∵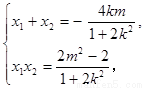
∴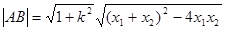
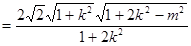 .
.
∵原点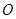 到直线
到直线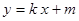 的距离
的距离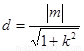 ,
,
∴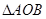 的面积
的面积
 .
.
∵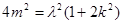 ,
,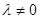 ,
,
∴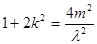 .
.
∴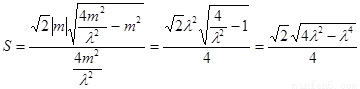
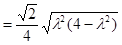 .
.
∵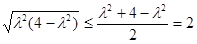 ,
,
∴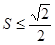 .
.
“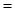 ”
成立
”
成立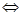
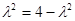 ,即
,即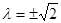 .
.
∴当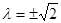 时,
时,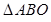 的面积最大,最大面积为
的面积最大,最大面积为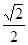
考点:直线和椭圆的相关问题,综合考查考生的运算求解能力.


科目:高中数学 来源: 题型:
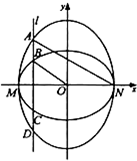 如图,已知MN分别是椭圆C1、C2的长轴和短轴,且C1、C2的离心率都等于
如图,已知MN分别是椭圆C1、C2的长轴和短轴,且C1、C2的离心率都等于
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(14分)已知![]() 、
、![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点,右焦点
的左、右焦点,右焦点![]() 到上顶点的距离为2,若
到上顶点的距离为2,若![]()
(1)求此椭圆的方程;
(2)点![]() 是椭圆的右顶点,直线
是椭圆的右顶点,直线![]() 与椭圆交于
与椭圆交于![]() 、
、![]() 两点(
两点(![]() 在第一象限内),又
在第一象限内),又![]() 、
、![]() 是此椭圆上两点,并且满足
是此椭圆上两点,并且满足 ,求证:向量
,求证:向量![]() 与
与![]() 共线
共线
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江西省高三模拟考试理科数学 题型:解答题
(12分)已知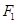 、
、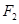 分别是椭圆
分别是椭圆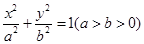 的左、右焦点,点B是其上顶点,椭圆的右准线与
的左、右焦点,点B是其上顶点,椭圆的右准线与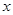 轴交于点N,且
轴交于点N,且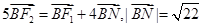 。
。
(1)求椭圆方程;
(2)直线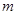 :
: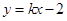 与椭圆交于不同的两点M、Q,若△BMQ是以MQ为底边的等腰三角形,求
与椭圆交于不同的两点M、Q,若△BMQ是以MQ为底边的等腰三角形,求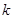 的值。
的值。
查看答案和解析>>
科目:高中数学 来源:2012届广东北江中学第一学期期末考试高二理科数学 题型:解答题
已知 、
、 分别是椭圆C:
分别是椭圆C:  的左焦点和右焦点,O是坐标系原点, 且椭圆C的焦距为6, 过
的左焦点和右焦点,O是坐标系原点, 且椭圆C的焦距为6, 过 的弦
的弦 两端点
两端点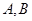 与
与 所成⊿
所成⊿ 的周长是
的周长是 .
.
(Ⅰ).求椭圆C的标准方程.
(Ⅱ) 已知点 ,
, 是椭圆C上不同的两点,线段
是椭圆C上不同的两点,线段 的中点为
的中点为 .
.
求直线 的方程;
的方程;
(Ⅲ)若线段 的垂直平分线与椭圆C交于点
的垂直平分线与椭圆C交于点 、
、 ,试问四点
,试问四点 、
、 、
、 、
、 是否在同一个圆上,若是,求出该圆的方程;若不是,请说明理由.
是否在同一个圆上,若是,求出该圆的方程;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com