练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数f（x）＝ax3+bx2﹣3x在x＝﹣1和x＝3处取得极值.

    （1）求a，b的值

    （2）求f（x）在[﹣4，4]内的最值.

    【答案】（1）a，b＝﹣1（2）f（x）min＝，f（x）max＝

    【解析】

    （1）先对函数求导，由题意可得＝3ax2+2bx﹣3＝0的两个根为﹣1和3，结合方程的根与系数关系可求，

    （2）由（1）可求，然后结合导数可判断函数的单调性，进而可求函数的最值.

    解：（1）＝3ax2+2bx﹣3，

    由题意可得＝3ax2+2bx﹣3＝0的两个根为﹣1和3，

    则，

    解可得a，b＝-1，

    （2）由（1），

    易得f（x）在，单调递增，在上单调递减，

    又f（﹣4），f（﹣1），f（3）＝﹣9，f（4），

    所以f（x）min＝f（﹣4），f（x）max＝f（﹣1）.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知，，其中.

    （Ⅰ）当时，求函数的单调区间；

    （Ⅱ）若恒成立，求的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆：的焦距为8，其短轴的两个端点与长轴的一个端点构成正三角形。

    （1）求的方程；

    （2）设为的左焦点，为直线上任意一点，过点作的垂线交于两点,.

    （i）证明：平分线段（其中为坐标原点）；

    （ii）当取最小值时，求点的坐标。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】过椭圆W:的左焦点作直线交椭圆于两点，其中 ，另一条过的直线交椭圆于两点（不与重合），且点不与点重合.过作轴的垂线分别交直线，于,.

    （Ⅰ）求点坐标和直线的方程；

    （Ⅱ）求证：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某日A, B, C三个城市18个销售点的小麦价格如下表：

    销售点序号

    所属城市

    小麦价格（元/吨）

    销售点序号

    所属城市

    小麦价格（元/吨）

    1

    A

    2420

    10

    B

    2500

    2

    C

    2580

    11

    A

    2460

    3

    C

    2470

    12

    A

    2460

    4

    C

    2540

    13

    A

    2500

    5

    A

    2430

    14

    B

    2500

    6

    C

    2400

    15

    B

    2450

    7

    A

    2440

    16

    B

    2460

    8

    B

    2500

    17

    A

    2460

    9

    A

    2440

    18

    A

    2540

    （Ⅰ）求B市5个销售点小麦价格的中位数；

    （Ⅱ）甲从B市的销售点中随机挑选一个购买1吨小麦，乙从C市的销售点中随机挑选一个购买1吨小麦，求甲花费的费用比乙高的概率；

    （Ⅲ）如果一个城市的销售点小麦价格方差越大，则称其价格差异性越大.请你对A、B、C三个城市按照小麦价格差异性从大到小进行排序（只写出结果）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某销售公司拟招聘一名产品推销员，有如下两种工资方案：

    方案一：每月底薪2000元，每销售一件产品提成15元；

    方案二：每月底薪3500元，月销售量不超过300件，没有提成，超过300件的部分每件提成30元．

    （1）分别写出两种方案中推销员的月工资（单位：元）与月销售产品件数的函数关系式；

    （2）从该销售公司随机选取一名推销员，对他（或她）过去两年的销售情况进行统计，得到如下统计表：

    月销售产品件数

    300

    400

    500

    600

    700

    次数

    2

    4

    9

    5

    4

    把频率视为概率，分别求两种方案推销员的月工资超过11090元的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)＝lnx﹣x2+ax，g(x)＝ex﹣e，其中a＞0.

    (1)若a＝1，证明：f(x)≤0；

    (2)用max{m，n}表示m和n中的较大值，设函数h(x)＝max{f(x)，g(x)}，讨论函数h(x)在(0，+∞)上的零点的个数.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    在平面直角坐标系中，直线的参数方程为（为参数，），以坐标原点为极点，以轴正半轴为极轴建立极坐标系，曲线的极坐标方程是.

    （1）求直线的普通方程和曲线的直角坐标方程；

    （2）已知直线与曲线交于两点，且，求实数的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校200名学生的数学期中考试成绩频率分布直方图如图所示，其中成绩分组区间是

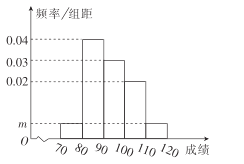
    （1）求图中的值；

    （2）根据频率分布直方图，估计这200名学生的平均分；

    （3）若这200名学生的数学成绩中，某些分数段的人数与英语成绩相应分数段的人数之比如表所示，求英语成绩在的人数.

    查看答案和解析>>

    同步练习册答案