
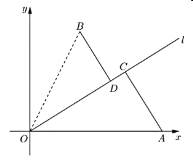
【题目】如图,已知城市![]() 周边有两个小镇
周边有两个小镇![]() 、
、![]() ,其中乡镇
,其中乡镇![]() 位于城市
位于城市![]() 的正东方
的正东方![]() 处,乡镇
处,乡镇![]() 与城市
与城市![]() 相距
相距![]() ,
,![]() 与
与![]() 夹角的正切值为2,为方便交通,现准备建设一条经过城市
夹角的正切值为2,为方便交通,现准备建设一条经过城市![]() 的公路
的公路![]() ,使乡镇
,使乡镇![]() 和
和![]() 分别位于
分别位于![]() 的两侧,过
的两侧,过![]() 和
和![]() 建设两条垂直
建设两条垂直![]() 的公路
的公路![]() 和
和![]() ,分别与公路
,分别与公路![]() 交汇于
交汇于![]() 、
、![]() 两点,以
两点,以![]() 为原点,
为原点,![]() 所在直线为
所在直线为![]() 轴,建立如图所示的平面直角坐标系
轴,建立如图所示的平面直角坐标系![]() .
.
(1)当两个交汇点![]() 、
、![]() 重合,试确定此时
重合,试确定此时![]() 路段长度;
路段长度;
(2)当![]() ,计算此时两个交汇点
,计算此时两个交汇点![]() 、
、![]() 到城市
到城市![]() 的距离之比;
的距离之比;
(3)若要求两个交汇点![]() 、
、![]() 的距离不超过
的距离不超过![]() ,求
,求![]() 正切值的取值范围.
正切值的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)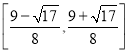 .
.
【解析】
(1)先求出直线![]() 的斜率为1,点B的坐标为
的斜率为1,点B的坐标为![]() ,再利用点到直线的距离为|BD|=
,再利用点到直线的距离为|BD|=![]() ;(2)设直线AB的斜率为
;(2)设直线AB的斜率为![]() ,先求出
,先求出![]() 再求出
再求出![]() ,即得
,即得![]() ;(3)先求出
;(3)先求出![]() ,再求出
,再求出![]() 解不等式即得解.
解不等式即得解.
(1)当两个交汇点![]() 、
、![]() 重合时,则AC,BD公路共线,
重合时,则AC,BD公路共线,
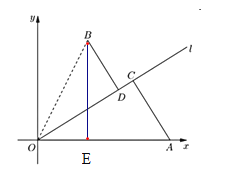
过点B作BE⊥AO,垂足为E, 则![]() ,
,
所以AE=![]() ,所以|BE|=|AE|,
,所以|BE|=|AE|,
所以直线AB的倾斜角为![]() ,所以直线AB的斜率为
,所以直线AB的斜率为![]() ,
,
所以直线![]() 的斜率为1,
的斜率为1,
因为点B的坐标为![]() ,所以|BD|=
,所以|BD|=![]() .
.
(2)由题得A(21,0),设直线AB的斜率为![]() ,
,
所以直线AB的方程为![]() ,
,
因为|AC|=|BD|,
所以![]() .
.
由题得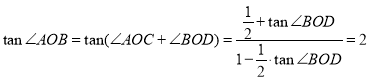 ,
,
所以![]() ,
,
所以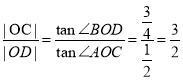 .
.
(3)由题得![]()
![]() ,
,
所以![]() ,
,
所以![]() .
.
因为![]() ,
,
所以![]()
解之得![]() .
.
故![]() 正切值的取值范围为
正切值的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】教材曾有介绍:圆![]() 上的点
上的点![]() 处的切线方程为
处的切线方程为![]() .我们将其结论推广:椭圆
.我们将其结论推广:椭圆![]() 上的点
上的点![]() 处的切线方程为
处的切线方程为![]() ,在解本题时可以直接应用.已知,直线
,在解本题时可以直接应用.已知,直线![]() 与椭圆
与椭圆![]() 有且只有一个公共点.
有且只有一个公共点.
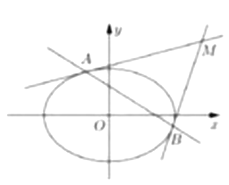
(1)求![]() 的值
的值
(2)设![]() 为坐标原点,过椭圆
为坐标原点,过椭圆![]() 上的两点
上的两点![]() 分别作该椭圆的两条切线
分别作该椭圆的两条切线![]() ,且
,且![]() 与
与![]() 交于点
交于点![]() .当
.当![]() 变化时,求
变化时,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】出租车几何学是由十九世纪的赫尔曼·闵可夫斯基所创立的.在出租车几何学中,点还是形如![]() 的有序实数对,直线还是满足
的有序实数对,直线还是满足![]() 的所有
的所有![]() 组成的图形,角度大小的定义也和原来一样,对于直角坐标系内任意两点
组成的图形,角度大小的定义也和原来一样,对于直角坐标系内任意两点![]() 、
、![]() 定义它们之间的一种“距离”(“直角距离”):
定义它们之间的一种“距离”(“直角距离”):![]() ,请解决以下问题:
,请解决以下问题:
(1)求线段![]() (
(![]() ,
,![]() )上一点
)上一点![]() 到原点
到原点![]() 的“距离”;
的“距离”;
(2)求所有到定点![]() 的“距离”均为2的动点围成的图形的周长;
的“距离”均为2的动点围成的图形的周长;
(3)在“欧式几何学”中有如下三个与“距离”有关的正确结论:
①平面上任意三点A,B,C,![]() ;
;
②平面上不在一直线上任意三点A,B,C,若![]() ,则
,则![]() 是以
是以![]() 为直角三角形
为直角三角形
③平面上存在两个不同的定点A,B,若动点P满足![]() ,则动点P的轨迹是
,则动点P的轨迹是![]() 的垂直平分线
的垂直平分线
上述结论对于“出租车几何学”中的直角距离是否还正确,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,圆
中,圆![]() :
:![]() ,直线
,直线![]() :
:![]() ,直线
,直线![]() 过点
过点![]() ,倾斜角为
,倾斜角为![]() ,以原点
,以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)写出直线![]() 与圆
与圆![]() 的交点极坐标及直线
的交点极坐标及直线![]() 的参数方程;
的参数方程;
(2)设直线![]() 与圆
与圆![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是甲、乙、丙三个企业的产品成本(单位:万元)及其构成比例,则下列判断正确的是( )

A. 乙企业支付的工资所占成本的比重在三个企业中最大
B. 由于丙企业生产规模大,所以它的其他费用开支所占成本的比重也最大
C. 甲企业本着勤俭创业的原则,将其他费用支出降到了最低点
D. 乙企业用于工资和其他费用支出额比甲丙都高
查看答案和解析>>
科目:高中数学 来源: 题型:
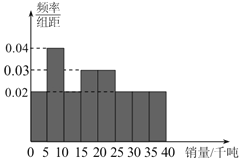
【题目】为了打好“精准扶贫攻坚战”某村扶贫书记打算带领该村农民种植新品种蔬菜,可选择的种植量有三种:大量种植,适量种植,少量种植.根据收集到的市场信息,得到该地区该品种蔬菜年销量频率分布直方图如图,然后,该扶贫书记同时调查了同类其他地区农民以往在各种情况下的平均收入如表1(表中收入单位:万元):
表1
销量 种植量 | 好 | 中 | 差 |
大量 |
| 8 | -4 |
适量 | 9 | 7 | 0 |
少量 | 4 | 4 | 2 |
但表格中有一格数据被墨迹污损,好在当时调查的数据频数分布表还在,其中大量种植的100户农民在市场销量好的情况下收入情况如表2:
收入(万元) | 11 | 11.5 | 12 | 12.5 | 13 | 13.5 | 14 | 14.5 | 15 |
频数(户) | 5 | 10 | 15 | 10 | 15 | 20 | 10 | 10 | 5 |
(Ⅰ)根据题中所给数据,请估计在市场销量好的情况下,大量种植的农民每户的预期收益.(用以往平均收入来估计);
(Ⅱ)若该地区年销量在10千吨以下表示销量差,在10千吨至30千吨之间表示销量中,在30千吨以上表示销量好,试根据频率分布直方图计算销量分别为好、中、差的概率(以频率代替概率);
(Ⅲ)如果你是这位扶贫书记,请根据(Ⅰ)(Ⅱ),从农民预期收益的角度分析,你应该选择哪一种种植量.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知不等式|2x-1|+|2x-2|<x+3的解集是A.
(Ⅰ)求集合A;
(Ⅱ)设x,y∈A,对任意a∈R,求证:xy(||x+a|-|y+a||)<x2+y2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】科研人员在对人体脂肪含量和年龄之间关系的研究中,获得了一些年龄和脂肪含量的简单随机样本数据,如下表:

根据上表的数据得到如下的散点图.
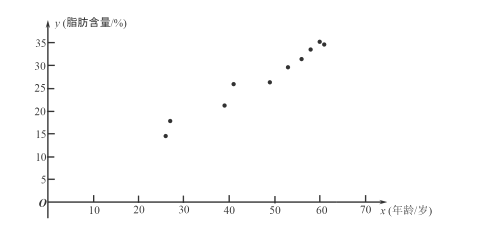
(1)根据上表中的样本数据及其散点图:
(i)求![]() ;
;
(ii)计算样本相关系数(精确到0.01),并刻画它们的相关程度.
(2)若y关于x的线性回归方程为![]() ,求
,求![]() 的值(精确到0.01),并根据回归方程估计年龄为50岁时人体的脂肪含量。
的值(精确到0.01),并根据回归方程估计年龄为50岁时人体的脂肪含量。
附:参考数据: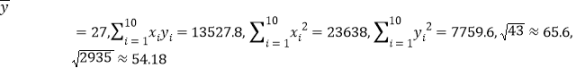
参考公式:相关系数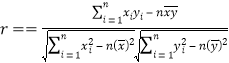
回归方程![]() 中斜率和截距的最小二乘估计公式分别为
中斜率和截距的最小二乘估计公式分别为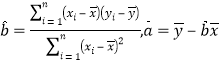
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com