
| A. | f(x)的图象关于($\frac{π}{12}$,1)中心对称 | B. | f(x)在($\frac{5π}{12}$,$\frac{11π}{12}$)上单调递减 | ||
| C. | f(x)的图象关于x=$\frac{π}{3}$对称 | D. | f(x)的最大值为3 |
分析 利用辅助角公式将函数进行化简,结合三角函数的单调性,最值性,对称性的性质分别进行判断即可.
解答 解:f(x)=$\sqrt{3}$sin2x-cos2x+1=2sin(2x-$\frac{π}{6}$)+1,
A.当x=$\frac{π}{12}$时,sin(2x-$\frac{π}{6}$)=0,则f(x)的图象关于($\frac{π}{12}$,1)中心对称,故A正确,
B.由2kπ+$\frac{π}{2}$≤2x-$\frac{π}{6}$≤2kπ+$\frac{3π}{2}$,k∈Z,得kπ+$\frac{π}{3}$≤x≤kπ+$\frac{5π}{6}$,k∈Z,
当k=0时,函数的递减区间是[$\frac{π}{3}$,$\frac{5π}{6}$],故B错误,
C.当x=$\frac{π}{3}$时,2x-$\frac{π}{6}$=2×$\frac{π}{3}$-$\frac{π}{6}$=$\frac{π}{2}$,则f(x)的图象关于x=$\frac{π}{3}$对称,故C正确,
D.当2sin(2x-$\frac{π}{6}$)=1时,函数取得最大值为2+1=3,故D正确,
故选:B
点评 本题主要考查与三角函数有关的命题的真假判断,利用辅助角公式将函数进行化简,结合三角函数的性质是解决本题的关键.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | (-3,1) | B. | $(\frac{3}{2},+∞)$ | C. | (-3,1)∪$(\frac{3}{2},+∞)$ | D. | $(-3,\frac{3}{2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
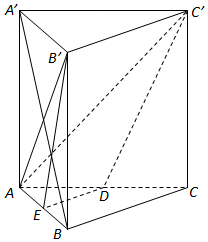 如图所示,直三棱柱ABC-A′B′C中,∠ABC=90°,AB=BC=BB′=2,D为底棱AC的中点.
如图所示,直三棱柱ABC-A′B′C中,∠ABC=90°,AB=BC=BB′=2,D为底棱AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{S_0}=\sqrt{S_1}+\sqrt{S_2}$ | B. | ${S_0}=\sqrt{{S_1}{S_2}}$ | C. | 2S0=S1+S2 | D. | S02=2S1S2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
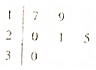 某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.
某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 2$\sqrt{3}$ | C. | 4 | D. | 4$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,0) | B. | ($\frac{1}{2}$,0) | C. | ($\frac{1}{8}$,0) | D. | (0,$\frac{1}{8}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com