在锐角△ABC中,角A、B、C的对边分别为a、b、c,已知2acosA=ccosB+bcosC.
(1)求A的大小;
(2)求cosB+cosC的取值范围.
解:(1)∵2acosA=ccosB+bcosC
∴由正弦定理,得2sinAcosA=sinCcosB+sinBcosC=sin(B+C)
∵△ABC中,B+C=π-A,∴2sinAcosA=sinA,得sinA(2cosA-1)=0
∵A∈(0,π),得sinA>0,∴2cosA-1=0,得cosA=

,得A=

(2)∵B+C=π-A=

,得C=

-B,
∴cosB+cosC=cosB+cos(

-B)=cosB+cos

cosB+sin

sinB=

cosB+

sinB=sin(B+

)
∵B是锐角△ABC的内角,可得B
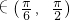
∴B+

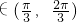
,可得sin(B+

)的最小值大于sin

=

当B=

时,sin(B+

)有最大值为1
由此可得,cosB+cosC的取值范围是(

,1].
分析:(1)根据正弦定理与两角和的正弦公式,将已知等式化简,得2sinAcosA=sin(B+C),结合三角形内角和定理与诱导公式,得2cosA-1=0,所以A=

;
(2)因为A=

,结合B是锐角△ABC的内角,可得B
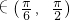
.再将cosB+cosC化简整理为sin(B+

),结合三角函数的图象与性质,不难得到cosB+cosC的取值范围.
点评:本题在锐角△ABC中,求两个角余弦和的取值范围.着重考查了正弦定理、两角和的正弦公式和三角函数的图象与性质等知识,属于基础题.

 ,得A=
,得A=
 ,得C=
,得C= -B,
-B, -B)=cosB+cos
-B)=cosB+cos cosB+sin
cosB+sin sinB=
sinB= cosB+
cosB+ sinB=sin(B+
sinB=sin(B+ )
)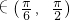

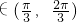 ,可得sin(B+
,可得sin(B+ )的最小值大于sin
)的最小值大于sin =
=
 时,sin(B+
时,sin(B+ )有最大值为1
)有最大值为1 ,1].
,1]. ;
; ,结合B是锐角△ABC的内角,可得B
,结合B是锐角△ABC的内角,可得B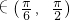 .再将cosB+cosC化简整理为sin(B+
.再将cosB+cosC化简整理为sin(B+ ),结合三角函数的图象与性质,不难得到cosB+cosC的取值范围.
),结合三角函数的图象与性质,不难得到cosB+cosC的取值范围.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案