
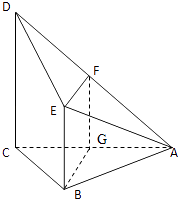
【题目】已知四棱锥A﹣BCDE,其中AB=BC=AC=BE=1,CD=2,CD⊥面ABC,BE∥CD,F为AD的中点.
(Ⅰ)求证:EF∥面ABC;
(Ⅱ)求证:平面ADE⊥平面ACD;
(Ⅲ)求四棱锥A﹣BCDE的体积.
【答案】证明:(Ⅰ)取AC中点G,连接FG、BG,∵F,G分别是AD,AC的中点
∴FG∥CD,且FG= ![]() DC=1.
DC=1.
∵BE∥CD∴FG与BE平行且相等
∴EF∥BG.
EF面ABC,BG面ABC
∴EF∥面ABC
(Ⅱ)∵△ABC为等边三角形∴BG⊥AC
又∵DC⊥面ABC,BG面ABC∴DC⊥BG
∴BG垂直于面ADC的两条相交直线AC,DC,
∴BG⊥面ADC.
∵EF∥BG
∴EF⊥面ADC
∵EF面ADE,∴面ADE⊥面ADC.
解:(Ⅲ)
方法一:连接EC,该四棱锥分为两个三棱锥E﹣ABC和E﹣ADC.![]() .
.
方法二:取BC的中点为O,连接AO,则AO⊥BC,又CD⊥平面ABC,
∴CD⊥AO,BC∩CD=C,∴AO⊥平面BCDE,
∴AO为VA﹣BCDE的高, ![]() ,∴
,∴ ![]() .
.
【解析】(Ⅰ)取AC中点G,连接FG、BG,根据三角形中位线定理,得到四边形FGBE为平行四边形,进而得到EF∥BG,再结合线面平行的判定定理得到EF∥面ABC;(Ⅱ)根据已知中△ABC为等边三角形,G为AC的中点,DC⊥面ABC得到BG⊥AC,DC⊥BG,根据线面垂直的判定定理得到BG⊥面ADC,则EF⊥面ADC,再由面面垂直的判定定理,可得面ADE⊥面ACD;(Ⅲ)方法一:四棱锥四棱锥A﹣BCDE分为两个三棱锥E﹣ABC和E﹣ADC,分别求出三棱锥E﹣ABC和E﹣ADC的体积,即可得到四棱锥A﹣BCDE的体积.
方法二:取BC的中点为O,连接AO,可证AO⊥平面BCDE,即AO为VA﹣BCDE的高,求出底面面积和高代入棱锥体积公式即可求出四棱锥A﹣BCDE的体积.
【考点精析】利用直线与平面平行的判定和平面与平面垂直的判定对题目进行判断即可得到答案,需要熟知平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一个平面过另一个平面的垂线,则这两个平面垂直.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源: 题型:
【题目】一个社会调查机构就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(如图).为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样方法抽出100人作进一步调查,则在[2500,3000)(元)月收入段应抽出人. 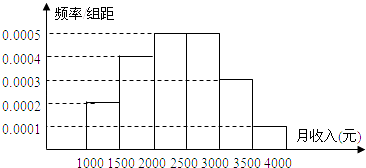
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2+2x+a=0上存在两点关于直线l:mx+y+1=0对称. (I)求m的值;
(Ⅱ)直线l与圆C交于A,B两点, ![]()
![]() =﹣3(O为坐标原点),求圆C的方程.
=﹣3(O为坐标原点),求圆C的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经过双曲线 ![]() ﹣
﹣ ![]() =1(a>0,b>0)的右焦点F作该双曲线一条渐近线的垂线与两条渐近线相交于M,N两点,若|MN|=
=1(a>0,b>0)的右焦点F作该双曲线一条渐近线的垂线与两条渐近线相交于M,N两点,若|MN|= ![]() ,则该双曲线的离心率是( )
,则该双曲线的离心率是( )
A.2或 ![]()
B.![]() 或
或 ![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某工厂对甲乙两个车间各10名工人生产的合格产品的统计结果的茎叶图.设甲、乙的中位数分别为x甲、x乙 , 甲、乙的方差分别为s甲2、s乙2 , 则( ) 
A.x甲<x乙 , s甲2<s乙2
B.x甲>x乙 , s甲2>s乙2
C.x甲>x乙 , s甲2<s乙2
D.x甲<x乙 , s甲2>s乙2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M:x2+(y﹣4)2=4,点P是直线l:x﹣2y=0上的一动点,过点P作圆M的切线PA,PB,切点为A,B.
(1)当切线PA的长度为 ![]() 时,求点P的坐标;
时,求点P的坐标;
(2)若△PAM的外接圆为圆N,试问:当P在直线l上运动时,圆N是否过定点?若存在,求出所有的定点的坐标;若不存在,说明理由.
(3)求线段AB长度的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xoy中,A为以原点O为圆心的单位圆O与x正半轴的交点,在圆心角为 ![]() 的扇形AOB的弧AB上任取一点 P,作 PN⊥OA于N,连结PO,记∠PON=θ.
的扇形AOB的弧AB上任取一点 P,作 PN⊥OA于N,连结PO,记∠PON=θ. 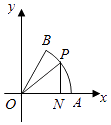
(1)设△PON的面积为y,使y取得最大值时的点P记为E,点N记为F,求此时 ![]() 的值;
的值;
(2)求k=a| ![]() ||
|| ![]() |+
|+ ![]() (a∈R,E 是在(1)条件下的点 E)的值域.
(a∈R,E 是在(1)条件下的点 E)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l过点P(2,3),根据下列条件分别求出直线l的方程:
(1)l在x轴、y轴上的截距之和等于0;
(2)l与两条坐标轴在第一象限所围城的三角形面积为16.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2cosx( ![]() sinx+cosx)+m,(x∈R,m∈R).
sinx+cosx)+m,(x∈R,m∈R).
(1)求f(x)的最小正周期;
(2)若f(x)在区间[0, ![]() ]上的最大值是6,求f(x)在区间[0,
]上的最大值是6,求f(x)在区间[0, ![]() ]上的最小值.
]上的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com