Question

【题目】函数f′（x）是奇函数f（x）（x∈R）的导函数，f（1）=0，当x＜0时，xf′（x）+f（x）＞0，则使得f（x）＜0成立的x的取值范围是（　　）
A.（﹣∞，﹣1）∪（0，1）
B.（﹣1，0）∪（1，+∞）
C.（﹣∞，﹣1）∪（1，+∞）
D.（﹣1，0）∪（0，1）

Answer 1

【答案】B
【解析】解：设g（x）=xf（x），则g′（x）=xf′（x）+f（x），
∵当x＜0时，xf′（x）+f（x）＞0，
∴则当x＜0时，g′（x）＞0，
∴函数g（x）=xf（x）在（﹣∞，0）上为增函数，
∵函数f（x）是奇函数，∴g（﹣x）=（﹣x）f（﹣x）=（﹣x）[﹣f（x）]=xf（x）=g（x），
∴函数g（x）为定义域上的偶函数，
由f（1）=0得，g（1）=0，函数g（x）的图象大致如右图：
∵不等式f（x）＜0＜0，
∴
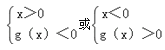
由函数的图象得，﹣1＜x＜0或x＞1，
∴使得f（x）＜0成立的x的取值范围是：（﹣1，0）∪（1，+∞），
故选：B．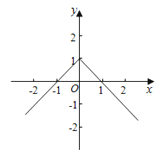

根据题意构造函数g（x）=xf（x），由求导公式和法则求出g′（x），结合条件判断出g′（x）的符号，即可得到函数g（x）的单调区间，根据f（x）奇函数判断出
g（x）是偶函数，将不等式进行转化，由图象求出不等式成立时x的取值范围．