
【题目】已知函数![]() 图像上一点
图像上一点![]() 处的切线方程为
处的切线方程为![]()
(1)求![]() 的值;
的值;
(2)若方程![]() 在区间
在区间![]() 内有两个不等实根,求
内有两个不等实根,求![]() 的取值范围;
的取值范围;
(3)令![]() 如果
如果![]() 的图像与
的图像与![]() 轴交于
轴交于![]() 两点,
两点,![]() 的中点为
的中点为![]() ,求证:
,求证:![]()
【答案】(1)![]() ;(2)
;(2)![]() ;(3)证明见解析
;(3)证明见解析
【解析】
(1)根据导数的几何意义可知![]() ,利用切线方程求得
,利用切线方程求得![]() ,代入曲线可得关于
,代入曲线可得关于![]() 的方程,与
的方程,与![]() 联立可构造方程组求得结果;(2)将问题转化为
联立可构造方程组求得结果;(2)将问题转化为![]() 与
与![]() 的图象在
的图象在![]() 上有两个交点;利用导数得到
上有两个交点;利用导数得到![]() 在
在![]() 上的单调性和最值,从而确定有两个交点时
上的单调性和最值,从而确定有两个交点时![]() 的取值范围,进而得到结果;(3)采用反证法,假设
的取值范围,进而得到结果;(3)采用反证法,假设![]() ,利用
,利用![]() 在
在![]() 上,中点坐标公式和
上,中点坐标公式和![]() 可化简整理得到
可化简整理得到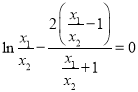 ,令
,令![]() ,构造函数
,构造函数![]() ,利用导数可知
,利用导数可知![]() 在
在![]() 上单调递增,从而得到
上单调递增,从而得到![]() ,与等式矛盾,可知假设不成立,从而证得结论.
,与等式矛盾,可知假设不成立,从而证得结论.
由题意得:![]() 定义域为
定义域为![]() ;
;![]()
(1)![]() 在
在![]() 处的切线方程为:
处的切线方程为:![]()
 ,解得:
,解得:![]()
(2)方程![]() 在区间
在区间![]() 内有两个不等实根等价于
内有两个不等实根等价于![]() 与
与![]() 的图象在
的图象在![]() 上有两个交点
上有两个交点
由(1)知:![]() ,
,![]()
![]() 当
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减
上单调递减 ![]()
又![]() ,
,![]()
![]() ,解得:
,解得:![]()
(3)![]() ,则
,则![]()
假设![]() ,则有:
,则有:
![]() …①;
…①;![]() …②;
…②;
![]() …③;
…③;![]() …④
…④
①![]() ②得:
②得:![]()
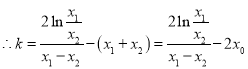
由④得:![]()
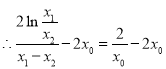 ,即:
,即: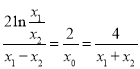
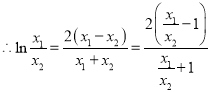 ,即
,即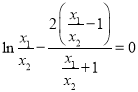
令![]() ,由
,由![]() 得:
得:![]()
设![]() ,
,![]()
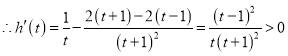
![]() 在
在![]() 上单调递增
上单调递增 ![]()
![]()
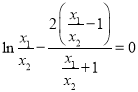 不成立,即假设不成立
不成立,即假设不成立
![]()


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:
【题目】高一(1)班参加校生物竞赛学生的成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题:

(1)求高一(1)班参加校生物竞赛的人数及分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间的矩形的高;
(2)若要从分数在[80,100]之间的学生中任选2人进行某项研究,求至少有1人分数在[90,100]之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角△ABC中,AC=![]() ,BC=1,点D是斜边AB上的动点,将△BCD沿着CD翻折至△B'CD,使得点B'在平面ACD内的射影H恰好落在线段CD上,则翻折后|AB'|的最小值是_____.
,BC=1,点D是斜边AB上的动点,将△BCD沿着CD翻折至△B'CD,使得点B'在平面ACD内的射影H恰好落在线段CD上,则翻折后|AB'|的最小值是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列判断正确的是( )
A.两圆锥曲线的离心率分别为![]() ,则“
,则“![]() ”是“两圆锥曲线均为椭圆”的充要条件.
”是“两圆锥曲线均为椭圆”的充要条件.
B.已知![]() 为圆
为圆![]() 内异于圆心的一点,则直线
内异于圆心的一点,则直线![]() 与该圆相交.
与该圆相交.
C.设![]() 是实数,若方程
是实数,若方程![]() 表示双曲线,则
表示双曲线,则![]() .
.
D.命题![]() 的否定是
的否定是![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年“中秋节”期间,高速公路车辆较多,交警部门通过路面监控装置抽样调查某一山区路段汽车行驶速度,采用的方法是:按到达监控点先后顺序,每隔50辆抽取一辆,总共抽取120辆,分别记下其行车速度,将行车速度(![]() )分成七段
)分成七段![]() 后得到如图所示的频率分布直方图,据图解答下列问题:
后得到如图所示的频率分布直方图,据图解答下列问题:
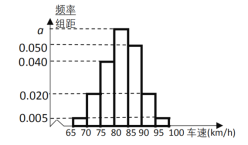
(1)求![]() 的值,并说明交警部门采用的是什么抽样方法?
的值,并说明交警部门采用的是什么抽样方法?
(2)求这120辆车行驶速度的众数和中位数的估计值(精确到0.1);
(3)若该路段的车速达到或超过![]() 即视为超速行驶,试根据样本估计该路段车辆超速行驶的概率.
即视为超速行驶,试根据样本估计该路段车辆超速行驶的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 图像上一点
图像上一点![]() 处的切线方程为
处的切线方程为![]()
(1)求![]() 的值;
的值;
(2)若方程![]() 在区间
在区间![]() 内有两个不等实根,求
内有两个不等实根,求![]() 的取值范围;
的取值范围;
(3)令![]() 如果
如果![]() 的图像与
的图像与![]() 轴交于
轴交于![]() 两点,
两点,![]() 的中点为
的中点为![]() ,求证:
,求证:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年年底,某城市地铁交通建设项目已经基本完成,为了解市民对该项目的满意度,分别从不同地铁站点随机抽取若干市民对该项目进行评分(满分
年年底,某城市地铁交通建设项目已经基本完成,为了解市民对该项目的满意度,分别从不同地铁站点随机抽取若干市民对该项目进行评分(满分![]() 分),绘制如下频率分布直方图,并将分数从低到高分为四个等级:
分),绘制如下频率分布直方图,并将分数从低到高分为四个等级:
满意度评分 | 低于60分 | 60分到79分 | 80分到89分 | 不低于90分 |
满意度等级 | 不满意 | 基本满意 | 满意 | 非常满意 |
已知满意度等级为基本满意的有![]() 人.
人.
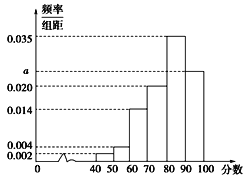
(1)求频率分布于直方图中![]() 的值,及评分等级不满意的人数;
的值,及评分等级不满意的人数;
(2)相关部门对项目进行验收,验收的硬性指标是:市民对该项目的满意指数不低于![]() ,否则该项目需进行整改,根据你所学的统计知识,判断该项目能否通过验收,并说明理由.
,否则该项目需进行整改,根据你所学的统计知识,判断该项目能否通过验收,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com