试题分析: 由
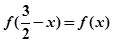
得:

,因为函数
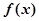
为奇函数,所以由

得:

,同理:

,

,所以
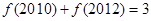
。故选C。
点评:本题是结合函数的性质,将
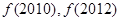
中的自变量变小,然后由已知的函数值得到他们的值。
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
已知函数
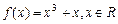
.
(I)指出
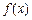
在定义域
R上的奇偶性与单调性(只须写出结论,无须证明);
(II)若
a、
b、
c∈
R,且
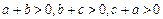
,试证明:
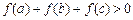
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数f(x)=(
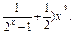
(1)求f(x)的定义域;
(2)讨论f(x)的奇偶性;
(3)证明:f(x)>0.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知函数
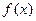
的周期为4,且当

时,
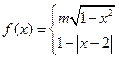
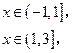
其中
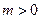
.若方程
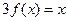
恰有5个实数解,则
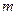
的

取值范围为 ( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数
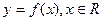
满足
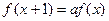
,
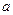
是不为
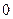
的实常数。
(1)若当
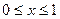
时,
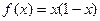
,求函数
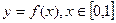
的值域;
(2)在(1)的条件下,求函数
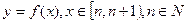
的解析式;
(3)若当
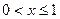
时,
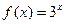
,试研究函数
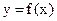
在区间
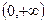
上是否可能是单调函数?
若可能,求出
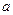
的取值范围;若不可能,请说明理由。
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数
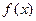
=
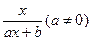
的图像过点(-4,4),且关于直线
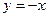
成轴对称图形,试确定
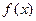
的解析式.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知
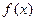
是R上的偶函数,对任意的
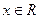
都有
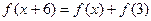
成立,若
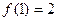
,则
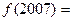
A 2007 B 2 C 1 D 0
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
设
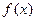
是定义在R上的以3为周期的奇函数,若
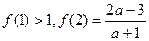
,则实数
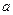
的取值范围是
。
查看答案和解析>>

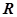 上的函数
上的函数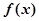 是奇函数且满足
是奇函数且满足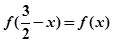 ,
,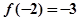 ,则
,则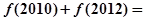 ( )
( )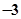
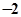
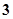
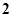
 教材全解字词句篇系列答案
教材全解字词句篇系列答案 满足
满足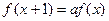 ,
,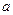 是不为
是不为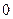 的实常数。
的实常数。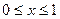 时,
时,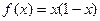 ,求函数
,求函数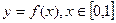 的值域;
的值域;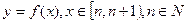 的解析式;
的解析式;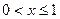 时,
时,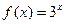 ,试研究函数
,试研究函数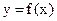 在区间
在区间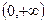 上是否可能是单调函数?
上是否可能是单调函数?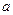 的取值范围;若不可能,请说明理由。
的取值范围;若不可能,请说明理由。