
ΓΨΧβΡΩΓΩΡ≥ΙΪΥΨΉΦ±ΗΫΪ1000Άρ‘ΣΉ ΫπΆΕ»ΥΒΫ –ΜΖ±ΘΙΛ≥ΧΫ®…η÷–Θ§œ÷”–ΦΉΘ§““ΝΫΗωΫ®…ηœνΡΩ―Γ‘ώΘ§»τΆΕΉ ΦΉœνΡΩ“ΜΡξΚσΩ…ΜώΒΟΒΡάϊ»σ![]() Θ®Άρ‘ΣΘ©ΒΡΗ≈¬ Ζ÷≤ΦΝ–»γ±μΥυ ΨΘΚ
Θ®Άρ‘ΣΘ©ΒΡΗ≈¬ Ζ÷≤ΦΝ–»γ±μΥυ ΨΘΚ
| 110 | 120 | 170 |
|
| 0.4 |
|
«“![]() ΒΡΤΎΆϊ
ΒΡΤΎΆϊ![]() ΘΜ»τΆΕΉ ““œνΡΩ“ΜΡξΚσΩ…ΜώΒΟΒΡάϊ»σ
ΘΜ»τΆΕΉ ““œνΡΩ“ΜΡξΚσΩ…ΜώΒΟΒΡάϊ»σ![]() Θ®Άρ‘ΣΘ©”κΗΟœνΡΩΫ®…η≤ΡΝœΒΡ≥…±Ψ”–ΙΊΘ§‘Ύ…ζ≤ζΒΡΙΐ≥Χ÷–Θ§ΙΪΥΨΫΪΗυΨί≥…±Ψ«ιΩωΨωΕ® «Ζώ‘ΎΒΎΕΰΚΆΒΎ»ΐΦΨΕ»Ϋχ––≤ζΤΖΒΡΦέΗώΒς’ϊΘ§ΝΫ¥ΈΒς’ϊœύΜΞΕάΝΔ«“Βς’ϊΒΡΗ≈¬ Ζ÷±πΈΣ
Θ®Άρ‘ΣΘ©”κΗΟœνΡΩΫ®…η≤ΡΝœΒΡ≥…±Ψ”–ΙΊΘ§‘Ύ…ζ≤ζΒΡΙΐ≥Χ÷–Θ§ΙΪΥΨΫΪΗυΨί≥…±Ψ«ιΩωΨωΕ® «Ζώ‘ΎΒΎΕΰΚΆΒΎ»ΐΦΨΕ»Ϋχ––≤ζΤΖΒΡΦέΗώΒς’ϊΘ§ΝΫ¥ΈΒς’ϊœύΜΞΕάΝΔ«“Βς’ϊΒΡΗ≈¬ Ζ÷±πΈΣ![]() ΚΆ
ΚΆ![]() .»τ““œνΡΩ≤ζΤΖΦέΗώ“ΜΡξΡΎΒς’ϊ¥Έ ΐ
.»τ““œνΡΩ≤ζΤΖΦέΗώ“ΜΡξΡΎΒς’ϊ¥Έ ΐ![]() Θ®¥Έ ΐΘ©”κ
Θ®¥Έ ΐΘ©”κ![]() ΒΡΙΊœΒ»γ±μΥυ ΨΘΚ
ΒΡΙΊœΒ»γ±μΥυ ΨΘΚ
| 0 | 1 | 2 |
| 41.2 | 117.6 | 204.0 |
Θ®1Θ©«σ![]() Θ§
Θ§![]() ΒΡ÷ΒΘΜ
ΒΡ÷ΒΘΜ
Θ®2Θ©«σ![]() ΒΡΖ÷≤ΦΝ–.
ΒΡΖ÷≤ΦΝ–.
 ÷«Μέ–ΓΗ¥œΑœΒΝ–¥πΑΗ
÷«Μέ–ΓΗ¥œΑœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣOΈΣΉχ±ξ‘≠ΒψΘ§≈ΉΈοœΏEΒΡΖΫ≥ΧΈΣx2ΘΫ2pyΘ®pΘΨ0Θ©Θ§ΤδΫΙΒψΈΣFΘ§ΙΐΒψM Θ®0Θ§4Θ©ΒΡ÷±œΏ![]() ”κ≈ΉΈοœΏœύΫΜ”ΎPΓΔQΝΫΒψ«“ΓςOPQΈΣ“‘OΈΣ÷±Ϋ«ΕΞΒψΒΡ÷±Ϋ«»ΐΫ«–ΈΘ°
”κ≈ΉΈοœΏœύΫΜ”ΎPΓΔQΝΫΒψ«“ΓςOPQΈΣ“‘OΈΣ÷±Ϋ«ΕΞΒψΒΡ÷±Ϋ«»ΐΫ«–ΈΘ°
Θ®ΔώΘ©«σEΒΡΖΫ≥ΧΘΜ
Θ®ΔρΘ©…ηΒψNΈΣ«ζœΏE…œΒΡ»Έ“β“ΜΒψΘ§÷ΛΟςΘΚ“‘FNΈΣ÷±ΨΕΒΡ‘≤”κx÷αœύ«–Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷Σ![]() ΤΫΟφ
ΤΫΟφ![]() ΤΫΟφ
ΤΫΟφ![]() ΈΣΒ»±Ώ»ΐΫ«–ΈΘ§
ΈΣΒ»±Ώ»ΐΫ«–ΈΘ§![]() ΈΣ
ΈΣ![]() ΒΡ÷–Βψ.
ΒΡ÷–Βψ.

Θ®1Θ©«σ÷ΛΘΚΤΫΟφ![]() ΤΫΟφ
ΤΫΟφ![]() ΘΜ
ΘΜ
Θ®2Θ©«σ÷±œΏ![]() ΚΆΤΫΟφ
ΚΆΤΫΟφ![]() Υυ≥…Ϋ«ΒΡ’ΐœ“÷Β.
Υυ≥…Ϋ«ΒΡ’ΐœ“÷Β.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
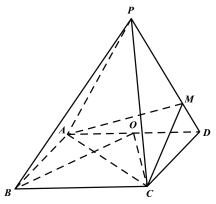
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΥΡάβΉΕPΘ≠ABCDΒΡΒΉΟφ «ΤΫ––ΥΡ±Ώ–ΈΘ§PDΓΆABΘ§O «ADΒΡ÷–ΒψΘ§BOΘΫCO.
Θ®1Θ©«σ÷ΛΘΚABΓΆΤΫΟφPADΘΜ
Θ®2Θ©»τADΘΫ2ABΘΫ4Θ§ PAΘΫPDΘ§ΒψM‘Ύ≤ύάβPD…œΘ§«“PDΘΫ3MDΘ§ΕΰΟφΫ«PΘ≠BCΘ≠DΒΡ¥σ–ΓΈΣ![]() Θ§«σ÷±œΏBP”κΤΫΟφMACΥυ≥…Ϋ«ΒΡ’ΐœ“÷Β.
Θ§«σ÷±œΏBP”κΤΫΟφMACΥυ≥…Ϋ«ΒΡ’ΐœ“÷Β.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() (a
(a![]() R)Θ§Τδ÷–eΈΣΉ‘»ΜΕ‘ ΐΒΡΒΉ ΐΘ°
R)Θ§Τδ÷–eΈΣΉ‘»ΜΕ‘ ΐΒΡΒΉ ΐΘ°
Θ®1Θ©»τ![]() Θ§«σΚ· ΐ
Θ§«σΚ· ΐ![]() ΒΡΒΞΒςΦθ«χΦδΘΜ
ΒΡΒΞΒςΦθ«χΦδΘΜ
Θ®2Θ©»τΚ· ΐ![]() ΒΡΕ®“ε”ρΈΣRΘ§«“
ΒΡΕ®“ε”ρΈΣRΘ§«“![]() Θ§«σaΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ§«σaΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®3Θ©÷ΛΟςΘΚΕ‘»Έ“β![]() Θ§«ζœΏ
Θ§«ζœΏ![]() …œ”–«“Ϋω”–»ΐΗω≤ΜΆ§ΒΡΒψΘ§‘Ύ’β»ΐΒψ¥ΠΒΡ«–œΏΨ≠ΙΐΉχ±ξ‘≠ΒψΘ°
…œ”–«“Ϋω”–»ΐΗω≤ΜΆ§ΒΡΒψΘ§‘Ύ’β»ΐΒψ¥ΠΒΡ«–œΏΨ≠ΙΐΉχ±ξ‘≠ΒψΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§»ΐάβ÷υ![]() ÷–Θ§≤ύάβ
÷–Θ§≤ύάβ![]() ΒΉΟφ
ΒΉΟφ![]() Θ§ΒΉΟφ»ΐΫ«–Έ
Θ§ΒΉΟφ»ΐΫ«–Έ![]() «’ΐ»ΐΫ«–ΈΘ§E «BC÷–ΒψΘ§‘ρœ¬Ν––π ω’ΐ»ΖΒΡ «Θ® Θ©
«’ΐ»ΐΫ«–ΈΘ§E «BC÷–ΒψΘ§‘ρœ¬Ν––π ω’ΐ»ΖΒΡ «Θ® Θ©

A.![]() ”κ
”κ![]() «“λΟφ÷±œΏB.
«“λΟφ÷±œΏB.![]() ΤΫΟφ
ΤΫΟφ![]()
C.AEΘ§![]() ΈΣ“λΟφ÷±œΏΘ§«“
ΈΣ“λΟφ÷±œΏΘ§«“![]() D.
D.![]() ΤΫΟφ
ΤΫΟφ![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() ΚΆΚ· ΐ
ΚΆΚ· ΐ![]() Θ§ΙΊ”Ύ’βΝΫΗωΚ· ΐΆΦœώΒΡΫΜΒψΗω ΐΘ§œ¬Ν–ΥΡΗωΫα¬έΘΚΔΌΒ±
Θ§ΙΊ”Ύ’βΝΫΗωΚ· ΐΆΦœώΒΡΫΜΒψΗω ΐΘ§œ¬Ν–ΥΡΗωΫα¬έΘΚΔΌΒ±![]() ±Θ§ΝΫΗωΚ· ΐΆΦœώΟΜ”–ΫΜΒψΘΜΔΎΒ±
±Θ§ΝΫΗωΚ· ΐΆΦœώΟΜ”–ΫΜΒψΘΜΔΎΒ±![]() ±Θ§ΝΫΗωΚ· ΐΆΦœώ«Γ”–»ΐΗωΫΜΒψΘΜΔέΒ±
±Θ§ΝΫΗωΚ· ΐΆΦœώ«Γ”–»ΐΗωΫΜΒψΘΜΔέΒ±![]() ±Θ§ΝΫΗωΚ· ΐΆΦœώ«Γ”–ΝΫΗωΫΜΒψΘΜΔήΒ±
±Θ§ΝΫΗωΚ· ΐΆΦœώ«Γ”–ΝΫΗωΫΜΒψΘΜΔήΒ±![]() ±Θ§ΝΫΗωΚ· ΐΆΦœώ«Γ”–ΥΡΗωΫΜΒψ.’ΐ»ΖΫα¬έΒΡΗω ΐΈΣΘ® Θ©
±Θ§ΝΫΗωΚ· ΐΆΦœώ«Γ”–ΥΡΗωΫΜΒψ.’ΐ»ΖΫα¬έΒΡΗω ΐΈΣΘ® Θ©
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§»ΐάβΉΕ![]() ÷–Θ§ΒΉΟφ
÷–Θ§ΒΉΟφ![]() «±Ώ≥ΛΈΣ2ΒΡ’ΐ»ΐΫ«–ΈΘ§
«±Ώ≥ΛΈΣ2ΒΡ’ΐ»ΐΫ«–ΈΘ§![]() Θ§
Θ§![]() ΒΉΟφ
ΒΉΟφ![]() Θ§Βψ
Θ§Βψ![]() Ζ÷±πΈΣ
Ζ÷±πΈΣ![]() Θ§
Θ§![]() ΒΡ÷–Βψ.
ΒΡ÷–Βψ.
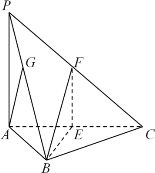
Θ®1Θ©«σ÷ΛΘΚΤΫΟφ![]() ΤΫΟφ
ΤΫΟφ![]() ΘΜ
ΘΜ
Θ®2Θ©‘ΎœΏΕΈ![]() …œ «Ζώ¥φ‘ΎΒψ
…œ «Ζώ¥φ‘ΎΒψ![]() Θ§ ΙΒΟ÷±œΏ
Θ§ ΙΒΟ÷±œΏ![]() ”κΤΫΟφ
”κΤΫΟφ![]() Υυ≥…ΒΡΫ«ΒΡ”ύœ“÷ΒΈΣ
Υυ≥…ΒΡΫ«ΒΡ”ύœ“÷ΒΈΣ![]() ΘΩ»τ¥φ‘ΎΘ§»ΖΕ®Βψ
ΘΩ»τ¥φ‘ΎΘ§»ΖΕ®Βψ![]() ΒΡΈΜ÷ΟΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”….
ΒΡΈΜ÷ΟΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”….
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈ“Ιζ « άΫγΒΎ“Μ≤ζΝΗ¥σΙζΘ§Έ“ΙζΝΗ ≥≤ζΝΩΚήΗΏΘ§’ϊΧεΚήΑ≤»ΪΑ¥’’14“Ύ»ΥΩΎΦΤΥψΘ§÷–Ιζ»ΥΨυΝΗ ≥≤ζΝΩ‘ΦΈΣ950Ϋο©¹±»»Ϊ«ρ»ΥΨυΝΗ ≥≤ζΝΩΗΏΝΥ‘Φ250ΫοΘ°»γΆΦ «÷–ΙζΙζΦ“Ά≥ΦΤΨ÷Άχ’Ψ÷–2010©¹2019ΡξΘ§Έ“ΙζΝΗ ≥≤ζΝΩΘ®«ßΆρΕ÷Θ©”κΡξΡ©Ήή»ΥΩΎΘ®«ßΆρ»ΥΘ©ΒΡΧθ–ΈΆΦΘ§ΗυΨί»γΆΦΩ…÷Σ‘Ύ2010©¹2019Ρξ÷–Θ® Θ©
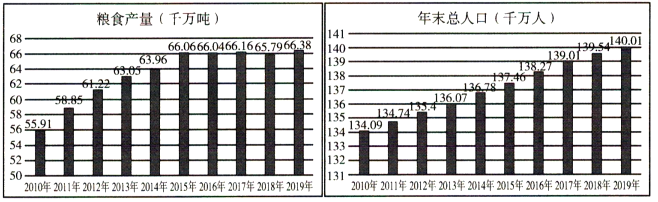
A.Έ“ΙζΝΗ ≥Ρξ≤ζΝΩ”κΡξΡ©Ήή»ΥΩΎΨυ÷πΡξΒί‘ω
B.2011ΡξΈ“ΙζΝΗ ≥Ρξ≤ζΝΩΒΡΡξ‘ω≥Λ¬ Ήν¥σ
C.2015Ρξ©¹2019ΡξΈ“ΙζΝΗ ≥Ρξ≤ζΝΩœύΕ‘Έ»Ε®
D.2015ΡξΈ“Ιζ»ΥΨυΝΗ ≥Ρξ≤ζΝΩ¥οΒΫΝΥΉνΗΏΖε
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com