


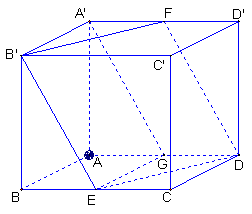
 如图所示,在平面ABCD内,过C作CP∥DE,交直线AD于P,则∠A′CP(或补角)为异面直线A′C与DE所成的角
如图所示,在平面ABCD内,过C作CP∥DE,交直线AD于P,则∠A′CP(或补角)为异面直线A′C与DE所成的角
 在△A′CP中,易得A′C=
在△A′CP中,易得A′C=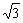 a,CP=DE=
a,CP=DE=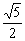 a,A′P=
a,A′P=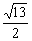 a
a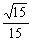
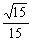

 ∵∠ADE=∠ADF,∴AD在平面B′EDF内的射影在∠EDF的平分线上(如图)又可证明四边形B′EDF为菱形(证明略),∴DB′为∠EDF的平分线,
∵∠ADE=∠ADF,∴AD在平面B′EDF内的射影在∠EDF的平分线上(如图)又可证明四边形B′EDF为菱形(证明略),∴DB′为∠EDF的平分线,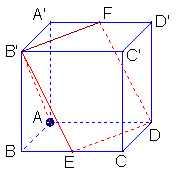 故直线AD与平面B′EDF所成的角为∠ADB′,
故直线AD与平面B′EDF所成的角为∠ADB′,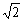 a,AB′=
a,AB′=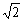 a,B′D=
a,B′D=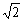 a,
a,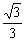 ,故AD与平面B′EDF所成的角是arccos
,故AD与平面B′EDF所成的角是arccos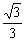

 (3)解
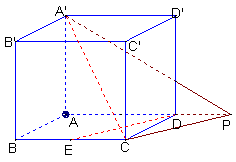
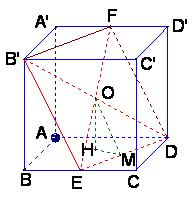
(3)解 如图,连结EF、B′D,交于O点,显然O为B′D的中点,从而O为正方形ABCD—A′B′C′D的中心,作OH⊥平面ABCD,则H为正方形ABCD的中心,再作HM⊥DE,垂足为M,连结OM,则OM⊥DE,故∠OMH为二面角B′—DE′—A的平面角
如图,连结EF、B′D,交于O点,显然O为B′D的中点,从而O为正方形ABCD—A′B′C′D的中心,作OH⊥平面ABCD,则H为正方形ABCD的中心,再作HM⊥DE,垂足为M,连结OM,则OM⊥DE,故∠OMH为二面角B′—DE′—A的平面角
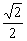 a,OD=
a,OD=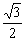 a,斜边DE=
a,斜边DE=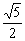 a,
a,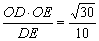 a
a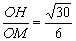
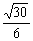


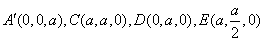
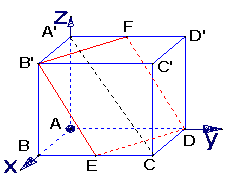
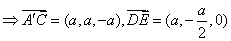

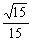

 如下图所示
如下图所示 又∵B′EDF为菱形,∴DB′为∠EDF的平分线,
又∵B′EDF为菱形,∴DB′为∠EDF的平分线,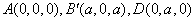
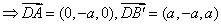
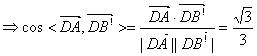 ,
,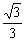

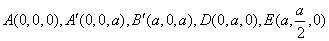 ,
,
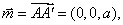 下面求面B′EDF的法向量
下面求面B′EDF的法向量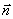

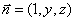 ,由
,由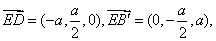
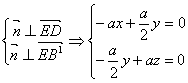
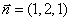
 ∴
∴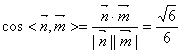 .
.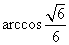

 求二面角的大小也可应用面积射影法
求二面角的大小也可应用面积射影法 点评:本题主要考查异面直线所成的角、线面角及二面角的一般求法,综合性较强
点评:本题主要考查异面直线所成的角、线面角及二面角的一般求法,综合性较强 用平移法求异面直线所成的角,利用三垂线定理求作二面角的平面角,是常用的方法.
用平移法求异面直线所成的角,利用三垂线定理求作二面角的平面角,是常用的方法.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
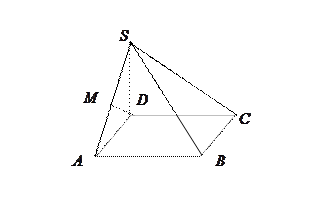 如图所示,四棱锥
如图所示,四棱锥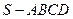 的底面是边长为1的正方形,
的底面是边长为1的正方形,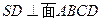 ,
,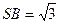 ,
,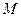 点是棱
点是棱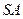 的中点。
的中点。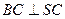 ;
;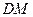 与
与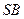 所成的角的大小;
所成的角的大小;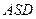 与面
与面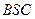 所成二面角的大小。
所成二面角的大小。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
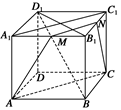
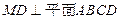 ,
,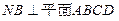 ,且MD=NB=1,E为BC的中点
,且MD=NB=1,E为BC的中点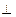 平面AMN?若存在,求线段AS的长;若不存在,请说明理由
平面AMN?若存在,求线段AS的长;若不存在,请说明理由


查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
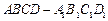 中,已知底面
中,已知底面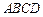 是边长为4的菱形,
是边长为4的菱形,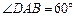 ,且点
,且点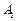 在面
在面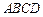 上的射影是底面对角线
上的射影是底面对角线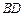 与AC的交点O,设点E是
与AC的交点O,设点E是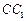 的中点,
的中点,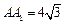 .
.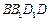 是矩形;
是矩形;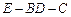 的大小;
的大小;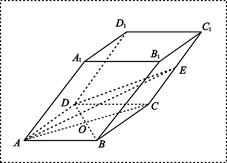 (Ⅲ) 求四面体
(Ⅲ) 求四面体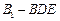 的体积.
的体积.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.平行于圆锥的一条母线的截面是等腰三角形 |
| B.平行于圆台的一条母线的截面是等腰梯形 |
| C.过圆锥顶点的截面是等腰三角形 |
| D.过圆台一个底面中心的截面是等腰梯形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com