
【题目】设函数f(x)=ax2-a-lnx,其中a ∈R.
(I)讨论f(x)的单调性;
(II)确定a的所有可能取值,使得![]() 在区间(1,+∞)内恒成立(e=2.718…为自然对数的底数)。
在区间(1,+∞)内恒成立(e=2.718…为自然对数的底数)。
【答案】(1) 当![]()
![]() 时,
时,![]() <0,
<0,![]() 单调递减;当
单调递减;当![]()
![]() 时,
时,![]() >0,
>0,![]() 单调递增;(2)
单调递增;(2) ![]() .
.
【解析】
试题分析:本题考查导数的计算、利用导数求函数的单调性,解决恒成立问题,考查学生的分析问题、解决问题的能力和计算能力.第(Ⅰ)问,对![]() 求导,再对a进行讨论,从而判断函数
求导,再对a进行讨论,从而判断函数![]() 的单调性;第(Ⅱ)问,利用导数判断函数的单调性,从而证明结论.
的单调性;第(Ⅱ)问,利用导数判断函数的单调性,从而证明结论.
试题解析:(Ⅰ)![]()
![]()
![]() <0,
<0,![]() 在
在![]() 内单调递减.
内单调递减.
![]() 由
由![]() =0,有
=0,有![]() .
.
此时,当![]()
![]() 时,
时,![]() <0,
<0,![]() 单调递减;
单调递减;
当![]()
![]() 时,
时,![]() >0,
>0,![]() 单调递增.
单调递增.
(Ⅱ)令![]() =
=![]() ,
,![]() =
=![]() .
.
则![]() =
=![]() .
.
而当![]() 时,
时,![]() >0,
>0,
所以![]() 在区间
在区间![]() 内单调递增.
内单调递增.
又由![]() =0,有
=0,有![]() >0,
>0,
从而当![]() 时,
时,![]() >0.
>0.
当![]() ,
,![]() 时,
时,![]() =
=![]() .
.
故当![]() >
>![]() 在区间
在区间![]() 内恒成立时,必有
内恒成立时,必有![]() .
.
当![]() 时,
时,![]() >1.
>1.
由(Ⅰ)有![]() ,从而
,从而![]() ,
,
所以此时![]() >
>![]() 在区间
在区间![]() 内不恒成立.
内不恒成立.
当![]() 时,令
时,令![]() ,
,
当![]() 时,
时,![]() ,
,
因此,![]() 在区间
在区间![]() 单调递增.
单调递增.
又因为![]() ,所以当
,所以当![]() 时,
时,![]() ,即
,即![]() 恒成立.
恒成立.
综上,![]() .
.


科目:高中数学 来源: 题型:
【题目】下表是一个容量为20的样本数据分组后的频率分布表:
分组 | [8.5,11.5] | [11.5,14.5] | [14.5,17.5] | [17.5,20.5] |
频数 | 4 | 2 | 6 | 8 |
(I)若用组中值代替本组数据的平均数,请计算样本的平均数![]() ;
;
(II)以频率估计概率,若样本的容量为2000,求在分组[14.5,17.5)中的频数;
(Ⅲ)若从数据在分组[8.5,11.5)与分组[11.5,14.5)的样本中随机抽取2个,求恰有1个样本落在分组[11.5,14.5)的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知各项均为正数的两个数列![]() 和{
和{![]() }满足:an+1=
}满足:an+1=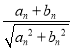 ,n∈N*.
,n∈N*.
(1)设bn+1=1+![]() ,n∈N*,求证:数列
,n∈N*,求证:数列![]() 是等差数列;
是等差数列;
(2)设bn+1=![]() ·
·![]() ,n∈N*,且
,n∈N*,且![]() 是等比数列,求a1和b1的值.
是等比数列,求a1和b1的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直三棱柱![]() 中,底面ABC为等腰直角三角形,
中,底面ABC为等腰直角三角形,![]() ,
,![]() ,
,![]() ,M是侧棱
,M是侧棱![]() 上一点,设
上一点,设![]() ,用空间向量知识解答下列问题.
,用空间向量知识解答下列问题.

![]() 1
1![]() 若
若![]() ,证明:
,证明:![]() ;
;
![]() 2
2![]() 若
若![]() ,求直线
,求直线![]() 与平面ABM所成的角的正弦值.
与平面ABM所成的角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数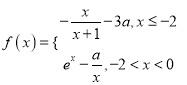 恰有3个零点,则实数
恰有3个零点,则实数![]() 的取值范围为( )
的取值范围为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】![]() ,在
,在![]() 上单调递减.若
上单调递减.若![]() ,则
,则![]() 在
在![]() 上递增,那么零点个数至多有一个,不符合题意,故
上递增,那么零点个数至多有一个,不符合题意,故![]() .故需
.故需![]() 当
当![]() 时
时![]() ,且
,且![]() ,使得第一段有一个零点,故
,使得第一段有一个零点,故![]() .对于第二段,
.对于第二段, ![]() ,故需
,故需![]() 在区间
在区间![]() 有两个零点,
有两个零点, ![]() ,故
,故![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,所以
上递减,所以 ,解得
,解得![]() .综上所述,
.综上所述, ![]()
【点睛】本小题主要考查函数的图象与性质,考查含有参数的分段函数零点问题的求解策略,考查了利用导数研究函数的单调区间,极值,最值等基本问题.其中用到了多种方法,首先对于第一段函数的分析利用了分离常数法,且直接看出函数的单调性.第二段函数利用的是导数来研究图像与性质.
【题型】单选题
【结束】
13
【题目】设![]() ,
, ![]() 满足约束条件
满足约束条件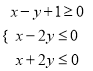 ,则
,则![]() 的最大值为_______.
的最大值为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是某省从1月21日至2月24日的新冠肺炎每日新增确诊病例变化曲线图.
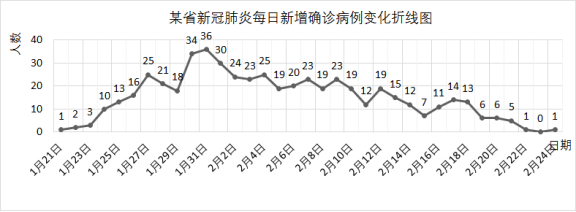
若该省从1月21日至2月24日的新冠肺炎每日新增确诊人数按日期顺序排列构成数列![]() ,
,![]() 的前n项和为
的前n项和为![]() ,则下列说法中正确的是( )
,则下列说法中正确的是( )
A.数列![]() 是递增数列B.数列
是递增数列B.数列![]() 是递增数列
是递增数列
C.数列![]() 的最大项是
的最大项是![]() D.数列
D.数列![]() 的最大项是
的最大项是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图![]() 所示,一条直角走廊宽为
所示,一条直角走廊宽为![]() ,
,![]()


(1)若位于水平地面上的一根铁棒在此直角走廊内,且![]() ,试求铁棒的长
,试求铁棒的长![]() ;
;
(2)若一根铁棒能水平地通过此直角走廊,求此铁棒的最大长度;
(3)现有一辆转动灵活的平板车,其平板面是矩形,它的宽![]() 为
为![]()
![]() 如图2.平板车若想顺利通过直角走廊,其长度
如图2.平板车若想顺利通过直角走廊,其长度![]() 不能超过多少米?
不能超过多少米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com