练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    (理)如果a1，a2，…，a8，为各项都大于零的等差数列，公差d≠0，则


    1. A.
      a1a8＞a4a5
    2. B.
      a1a8＜a4a5
    3. C.
      a1+a8＞a4+a5
    4. D.
      a1a8＝a4a5
    B
    B设等差数列公差为d，则a1a8-a4a5＝a1(a1+7d)-(a1+3d)(a1+4d)＝-12d2＜0，所以a1a8＜a4a5，本题易错选为D，其原因为将等比数列的有关性质运用在了等差数列中，这是公式混淆所致．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：教材完全解读　高中数学　必修5(人教B版课标版) 人教B版课标版 题型：013

    (理)如果a1，a2，…，a8，为各项都大于零的等差数列，公差d≠0，则

    [　　]

    A．a1a8＞a4a5

    B．a1a8＜a4a5

    C．a1＋a8＞a4＋a5

    D．a1a8＝a4a5

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    (理)如果有穷数列a1,a2,a3,…,an(n为正整数)满足条件a1=an,a2=an-1,…,an=a1,即ai=an-i+1(i=1,2,…,n),我们称其为“对称数列”.例如,由组合数组成的数列,,…,就是“对称数列”.

    (1)设{bn}是项数为7的“对称数列”,其中b1,b2,b3,b4是等差数列,且b1=2,b4=11.依次写出{bn}的每一项.

    (2)设{cn}是项数为2k-1(正整数k＞1)的“对称数列”,其中ck,ck+1,…,c2k-1是首项为50,公差为-4的等差数列.记{cn}各项的和为S2k-1,当k为何值时,S2k-1取得最大值?并求出S2k-1的最大值.

    (3)对于确定的正整数m＞1,写出所有项数不超过2m的“对称数列”,使得1,2,22,…,2m-1依次是该数列中连续的项;当m＞1 500时,求其中一个“对称数列”前2 008项的和S2008.

    (文)如果有穷数列a1,a2,a3,…,am(m为正整数)满足条件a1=am,a2=am-1,…,am=a1,即ai=am-i+1(i=1,2,…,m),我们称其为“对称数列”.例如,数列1,2,5,2,1与数列8,4,2,2,4,8都是“对称数列”.

    (1)设{bn}是7项的“对称数列”,其中b1,b2,b3,b4是等差数列,且b1=2,b4=11.依次写出{bn}的每一项;

    (2)设{cn}是49项的“对称数列”,其中c25,c26,…,c49是首项为1,公比为2的等比数列,求{cn}各项的和S;

    (3)设{dn}是100项的“对称数列”,其中d51,d52,…,d100是首项为2,公差为3的等差数列,求{dn}前n项的和Sn(n=1,2,…,100).

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012江西理）

    如图,从A1(1,0,0),A2(2,0,0),B1(0,2,0),B2(0,2,0),C1(0,0,1),C2(0,0,2)这6个点中随机选取3个点,将这3个点及原点O两两相连构成一个“立体”,记该“立体”的体积为随机变量V(如果选取的3个点与原点在同一个平面内,此时“立体”的体积V=0).

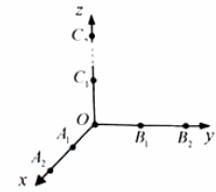
    (1)求V=0的概率;

    (2)求V的分布列及数学期望.

    查看答案和解析>>

    同步练习册答案