
【题目】现有0、1、2、3、4、5、6、7、8、9共十个数字.
(1)可以组成多少个无重复数字的三位数?
(2)组成无重复数字的三位数中,315是从小到大排列的第几个数?
(3)可以组成多少个无重复数字的四位偶数?
(4)选出一个偶数和三个奇数,组成无重复数字的四位数,这样的四位数共有多少个?
(5)如果一个数各个数位上的数字从左到右按由大到小的顺序排列,则称此正整数为“渐减数”, 那么由这十个数字组成的所有“渐减数”共有多少个?
【答案】(1)648;(2)156;(3)2296;(4)1140;(5)1013
【解析】
(1)百位不为0,后两位排任意数即可;
(2)分当百位分别是1、2、3时数的个数,找到315的位置;
(3)分当个位上是0和当个位上是2,4,6,8中的一个时两种情况分别求出排列数即可;
(4)分当选出的偶数是0和不是0两种情况分别求出排列数即可;
(5)由题意,渐减数至少是两位数,当选出数时排列顺序是固定的,所以分别表示出两位数、三位数、![]() 、十位数时渐减数的个数,再利用二项式系数的和求解即可.
、十位数时渐减数的个数,再利用二项式系数的和求解即可.
(1)由题意,无重复的三位数共有![]() 个;
个;
(2)当百位为1时,共有![]() 个数;
个数;
当百位为2时,共有![]() 个数;
个数;
当百位为3时,共有![]() 个数,
个数,
所以315是第![]() 个数;
个数;
(3)无重复的四位偶数,所以个位必须为0,2,4,6,8,千位上不能为0,
当个位上为0时,共有![]() 个数;
个数;
当个位上是2,4,6,8中的一个时,共有![]() 个数,
个数,
所以无重复的四位偶数共有![]() 个数;
个数;
(4)当选出的偶数为0时,共有![]() 个数,
个数,
当选出的偶数不为0时,共有![]() 个数,
个数,
所以这样的四位数共有![]() 个数;
个数;
(5)当挑出两个数时,渐减数共有![]() 个,
个,
当挑出三个数时,渐减数共有![]() 个,
个,
![]() ,
,
当挑出十个数时,渐减数共有![]() 个,
个,
所以这样的数共有![]() 个.
个.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源: 题型:
【题目】在吸烟与患肺病这两个分类变量的计算中,下列说法正确的是( )
A.若![]() 的观测值为6.635,我们有
的观测值为6.635,我们有![]() 的把握认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病
的把握认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病
B.从独立性检验可知有![]() 的把握认为吸烟与患肺病有关系时,我们就说某人吸烟,那么他有
的把握认为吸烟与患肺病有关系时,我们就说某人吸烟,那么他有![]() 的可能患有肺病
的可能患有肺病
C.若从统计量中求出有![]() 的把握认为吸烟与患肺病有关系,是指有
的把握认为吸烟与患肺病有关系,是指有![]() 的可能性使得推断出现错误
的可能性使得推断出现错误
D.以上三种说法都不正确
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )
A. 1盏 B. 3盏 C. 5盏 D. 9盏
查看答案和解析>>
科目:高中数学 来源: 题型:
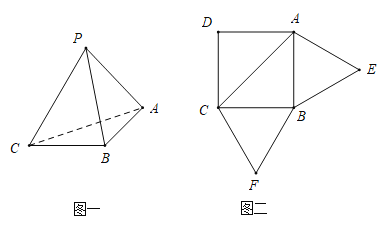
【题目】已知三棱锥![]() 的展开图如图二,其中四边形
的展开图如图二,其中四边形![]() 为边长等于
为边长等于![]() 的正方形,
的正方形,![]() 和
和![]() 均为正三角形,在三棱锥
均为正三角形,在三棱锥![]() 中:
中:
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() 是
是![]() 的中点,求二面角
的中点,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com