
【题目】已知椭圆![]() ,左、右顶点分别为
,左、右顶点分别为![]() ,
,![]() ,上、下顶点分别为
,上、下顶点分别为![]() ,
,![]() ,且
,且![]() ,
,![]() 为等边三角形,过点
为等边三角形,过点![]() 的直线与椭圆
的直线与椭圆![]() 在
在![]() 轴右侧的部分交于
轴右侧的部分交于![]() 、
、![]() 两点,
两点,![]() 为坐标原点.
为坐标原点.

(1)求椭圆的标准方程;
(2)求![]() 面积的取值范围.
面积的取值范围.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某医院为筛查某种疾病,需要检验血液是否为阳性,现有![]() 份血液样本,有以下两种检验方式:①逐份检验,列需要检验
份血液样本,有以下两种检验方式:①逐份检验,列需要检验![]() 次;②混合检验,将其
次;②混合检验,将其![]() (
(![]() 且
且![]() )份血液样本分别取样混合在一起检验.若检验结果为阴性,这
)份血液样本分别取样混合在一起检验.若检验结果为阴性,这![]() 份的血液全为阴性,因而这
份的血液全为阴性,因而这![]() 份血液样本只要检验一次就够了,如果检验结果为阳性,为了明确这
份血液样本只要检验一次就够了,如果检验结果为阳性,为了明确这![]() 份血液究竟哪几份为阳性,就要对这
份血液究竟哪几份为阳性,就要对这![]() 份再逐份检验,此时这
份再逐份检验,此时这![]() 份血液的检验次数总共为
份血液的检验次数总共为![]() 次.假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为
次.假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为![]() .
.
(1)假设有5份血液样本,其中只有2份样本为阳性,若采用逐份检验的方式,求恰好经过3次检验就能把阳性样本全部检验出来的概率.
(2)现取其中![]() (
(![]() 且
且![]() )份血液样本,记采用逐份检验方式,样本需要检验的总次数为
)份血液样本,记采用逐份检验方式,样本需要检验的总次数为![]() ,采用混合检验方式,样本需要检验的总次数为
,采用混合检验方式,样本需要检验的总次数为![]() .
.
(i)运用概率统计的知识,若![]() ,试求
,试求![]() 关于
关于![]() 的函数关系式
的函数关系式![]() ;
;
(ii)若![]() ,且采用混合检验方式可以使得样本需要检验的总次数的期望值比逐份检验的总次数期望值更少,求
,且采用混合检验方式可以使得样本需要检验的总次数的期望值比逐份检验的总次数期望值更少,求![]() 的最大值.
的最大值.
参考数据:![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年空气质量逐步恶化,雾霾天气现象出现增多,大气污染危害加重. 大气污染可引起心悸、呼吸困难等心肺疾病。为了解某市心肺疾病是否与性别有关,在某医院随机的对入院50人进行了问卷调查得到了如在的列联表:已知在全部50人中随机抽取1人,抽到患心肺疾病的人的概率为![]() .
.
(Ⅰ)请将右面的列联表补充完整;
患心肺疾病 | 不患心肺疾病 | 合计 | |
男 | 5 | ||
女 | 10 | ||
合计 | 50 |
(Ⅱ)是否有99.5%的把握认为患心肺疾病与性别有关?说明你的理由;
(Ⅲ)已知在患心肺疾病的10位女性中,有3位又患胃病.现在从患心肺疾病的10位女性中,选出3名进行其他方面的排查,记选出患胃病的女性人数为![]() ,求
,求![]() 的分布列以及数学期望.
的分布列以及数学期望.
下面的临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式![]() 其中
其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双曲线![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() ,
,![]() 为坐标原点.
为坐标原点.![]() 为曲线
为曲线![]() 右支上的点,点
右支上的点,点![]() 在
在![]() 外角平分线上,且
外角平分线上,且![]() .若
.若![]() 恰为顶角为
恰为顶角为![]() 的等腰三角形,则该双曲线的离心率为( )
的等腰三角形,则该双曲线的离心率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古典乐器一般按“八音”分类.“八音”是我国最早按乐器的制造材料来对乐器进行分类的方法,最先见于《周礼·春官·大师》,分为“金、石、土、革、丝、木、匏(páo)、竹”八音.其中“金、石、木、革”为打击乐器,“土、匏、竹”为吹奏乐器,“丝”为弹拨乐器,现从打击乐器、弹拨乐器中任取不同的‘两音’,含有弹拨乐器的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点
的焦点![]() ,过其准线与
,过其准线与![]() 轴的交点
轴的交点![]() 作直线
作直线![]() ,
,
(1)若直线![]() 与抛物线相切于点
与抛物线相切于点![]() ,则
,则![]() =_____________.
=_____________.
(2)设![]() ,若直线
,若直线![]() 与抛物线交于点
与抛物线交于点![]() ,且
,且![]() ,则
,则![]() =_____________.
=_____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】金秋九月,丹桂飘香,某高校迎来了一大批优秀的学生.新生接待其实也是和社会沟通的一个平台.校团委、学生会从在校学生中随机抽取了160名学生,对是否愿意投入到新生接待工作进行了问卷调查,统计数据如下:
愿意 | 不愿意 | |
男生 | 60 | 20 |
女士 | 40 | 40 |
(1)根据上表说明,能否有99%把握认为愿意参加新生接待工作与性别有关;
(2)现从参与问卷调查且愿意参加新生接待工作的学生中,采用按性别分层抽样的方法,选取10人.若从这10人中随机选取3人到火车站迎接新生,设选取的3人中女生人数为![]() ,写出
,写出![]() 的分布列,并求
的分布列,并求![]() .
.
附: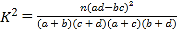 ,其中
,其中![]() .
.
| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com