
【题目】设函数![]() 是定义在
是定义在![]() 上的偶函数,且对任意的
上的偶函数,且对任意的![]() 恒有
恒有![]() ,已知当
,已知当![]() 时,
时,![]() ,则下列命题:
,则下列命题:
①对任意![]() ,都有
,都有![]() ;②函数
;②函数![]() 在
在![]() 上递减,在
上递减,在![]() 上递增;
上递增;
③函数![]() 的最大值是1,最小值是0;④当
的最大值是1,最小值是0;④当![]() 时,
时,![]() .
.
其中正确命题的序号有________.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 表示两个不同的平面,
表示两个不同的平面, ![]() 表示两条不同直线,对于下列两个命题:
表示两条不同直线,对于下列两个命题:
①若![]() ,则“
,则“![]() ”是“
”是“![]() ”的充分不必要条件;
”的充分不必要条件;
②若![]() ,则“
,则“![]() ”是“
”是“![]() 且
且![]() ”的充要条件.判读正确的是( )
”的充要条件.判读正确的是( )
A. ①②都是真命题 B. ①是真命题,②是假命题
C. ①是假命题,②是真命题 D. ①②都是假命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,已知曲线C1:ρ=2cosθ,将曲线C1上的点向左平移一个单位,然后纵坐标不变,横坐标伸长到原来的2倍,得到曲线C,又已知直线l: 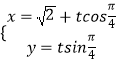 (t是参数),且直线l与曲线C交于A,B两点.
(t是参数),且直线l与曲线C交于A,B两点.
(1)求曲线C的直角坐标方程,并说明它是什么曲线;
(2)设定点P( ![]() ,0),求|PA|+|PB|.
,0),求|PA|+|PB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 为偶函数,且函数
为偶函数,且函数![]() 图象的两相邻对称轴间的距离为
图象的两相邻对称轴间的距离为![]() .
.
(1)求![]() 的值;
的值;
(2)求函数![]() 的对称轴方程;
的对称轴方程;
(3)当![]() 时,方程
时,方程![]() 有两个不同的实根,求m的取值范围。
有两个不同的实根,求m的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经过市场调查,超市中的某种小商品在过去的近40天的日销售量(单位:件)与价格(单位:元)为时间![]() (单位:天)的函数,且日销售量近似满足
(单位:天)的函数,且日销售量近似满足![]() ,价格近似满足
,价格近似满足![]() 。
。
(1)写出该商品的日销售额![]() (单位:元)与时间
(单位:元)与时间![]() (
(![]() )的函数解析式并用分段函数形式表示该解析式(日销售额=销售量
)的函数解析式并用分段函数形式表示该解析式(日销售额=销售量![]() 商品价格);
商品价格);
(2)求该种商品的日销售额![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018河北保定市上学期期末调研】已知点![]() 到点
到点![]() 的距离比到
的距离比到![]() 轴的距离大1.
轴的距离大1.
(I)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(II)设直线![]() :
: ![]() ,交轨迹
,交轨迹![]() 于
于![]() 、
、![]() 两点,
两点, ![]() 为坐标原点,试在轨迹
为坐标原点,试在轨迹![]() 的
的![]() 部分上求一点
部分上求一点![]() ,使得
,使得![]() 的面积最大,并求其最大值.
的面积最大,并求其最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:
①函数![]() 的单调增区间是
的单调增区间是![]() ;
;
②若函数![]() 定义域为
定义域为![]() 且满足
且满足![]() ,则它的图象关于
,则它的图象关于![]() 轴对称;
轴对称;
③函数![]() 的值域为
的值域为![]() ;
;
④函数![]() 的图象和直线
的图象和直线![]() 的公共点个数是
的公共点个数是![]() ,则
,则![]() 的值可能是
的值可能是![]() ;
;
⑤若函数![]() 在
在![]() 上有零点,则实数
上有零点,则实数![]() 的取值范围是
的取值范围是![]() .
.
其中正确的序号是_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com