
分析 (Ⅰ)点P在函数$y=\frac{1}{1-x}$的图象上,可得点$P({\frac{1}{2},2})$,利用相互垂直的直线斜率之间的关系即可得出.
(Ⅱ)点P(m,n)在直线l0上,可得m+2n+4=0,即m=-2n-4,代入mx+(n-1)y+n+5=0中,整理得n(-2x+y+1)-(4x+y-5)=0,由$\left\{\begin{array}{l}-2x+y+1=0\\ 4x+y-5=0\end{array}\right.$,解得即可得出.
解答 解:(Ⅰ)点P在函数$y=\frac{1}{1-x}$的图象上,$n=\frac{1}{1-m}=2$,即点$P({\frac{1}{2},2})$…(2分)
由x+2y+4=0,得$y=-\frac{1}{2}x-2$,即直线l0的斜率为$-\frac{1}{2}$,
又直线l与直线l0垂直,则直线l的斜率k满足:$-\frac{1}{2}k=-1$,即k=2,…(4分)
所以直线l的方程为$y-2=2({x-\frac{1}{2}})$,一般式方程为:2x-y+1=0.…(6分)
(Ⅱ)点P(m,n)在直线l0上,所以m+2n+4=0,即m=-2n-4,…(8分)
代入mx+(n-1)y+n+5=0中,整理得n(-2x+y+1)-(4x+y-5)=0,…(10分)
由$\left\{\begin{array}{l}-2x+y+1=0\\ 4x+y-5=0\end{array}\right.$,解得$\left\{\begin{array}{l}x=1\\ y=1\end{array}\right.$,
故直线mx+(n-1)y+n+5=0必经过定点,其坐标为(1,1).…(12分)
点评 本题考查了直线相互垂直的充要条件、直线系的应用,考查了推理能力与计算能力,属于中档题.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:解答题
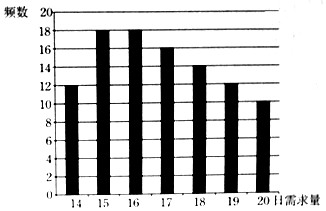 某蛋糕店每天制作生日蛋糕若干个,每个生日蛋糕成本为50元,每个蛋糕的售价为100元,如果当天卖不完,剩余的蛋糕作垃圾处理.现搜集并整理了100天生日蛋糕的日需求量(单位:个),得到如图所示的柱状图.100天记录的各需求量的频率作为每天各需求量发生的概率.
某蛋糕店每天制作生日蛋糕若干个,每个生日蛋糕成本为50元,每个蛋糕的售价为100元,如果当天卖不完,剩余的蛋糕作垃圾处理.现搜集并整理了100天生日蛋糕的日需求量(单位:个),得到如图所示的柱状图.100天记录的各需求量的频率作为每天各需求量发生的概率.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,1) | B. | [-2,1] | C. | [-2,-1) | D. | [-1,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,4,5} | B. | {2,3} | C. | {4,5} | D. | {1,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
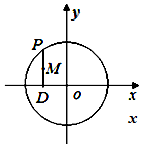 如图,在圆x2+y2=16上任取一点P,过点P作x 轴的垂线段PD,D为垂足,当点P在圆上运动时,则线段PD的中点M的轨迹方程为$\frac{x^2}{16}+\frac{y^2}{4}=1$.
如图,在圆x2+y2=16上任取一点P,过点P作x 轴的垂线段PD,D为垂足,当点P在圆上运动时,则线段PD的中点M的轨迹方程为$\frac{x^2}{16}+\frac{y^2}{4}=1$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
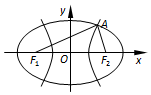 如图,F1,F2是椭圆C1与双曲线C2的公共焦点,点A是C1,C2的公共点.设C1,C2的离心率分别是e1,e2,∠F1AF2=2θ,则( )
如图,F1,F2是椭圆C1与双曲线C2的公共焦点,点A是C1,C2的公共点.设C1,C2的离心率分别是e1,e2,∠F1AF2=2θ,则( )| A. | ${e_1}^2{sin^2}θ+{e_2}^2{cos^2}θ=e_1^2e_2^2$ | |
| B. | ${e_2}^2{sin^2}θ+{e_1}^2{cos^2}θ=e_1^2e_2^2$ | |
| C. | ${e_2}^2{sin^2}θ+{e_1}^2{cos^2}θ=1$ | |
| D. | ${e_1}^2{sin^2}θ+{e_2}^2{cos^2}θ=1$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com