解:(Ⅰ)由题意得f'(x)=3ax
2-12ax+3b,f'(2)=-3,
∵图象在x=2处的切线方程为3x+y-11=0.
∴x=2时,y=5,即f(2)=5,
∴
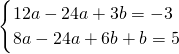
即
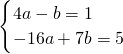
解得a=1,b=3,
∴f(x)=x
3-6x
2+9x+3.(4分)
(Ⅱ)由f(x)=x
3-6x
2+9x+3,可得f'(x)=3x
2-12x+9,
∴
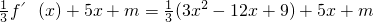
=x
2+x+3+m,
则由题意可得x
3-6x
2+9x+3=x
2+x+3+m有三个不相等的实根,
即g(x)=x
3-7x
2+8x-m的图象与x轴有三个不同的交点,g'(x)=3x
2-14x+8=(3x-2)(x-4),
则g(x),g'(x)的变化情况如下表.
| x | 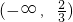 |  | 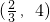 | 4 | (4,+∞) |
| g'(x) | + | 0 | - | 0 | + |
| g(x) | ↗ | 极大值 | ↘ | 极小值 | ↗ |
则函数f(x)的极大值为

,极小值为g(4)=-16-m.(6分)
y=f(x)的图象与
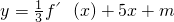
的图象有三个不同交点,则有:
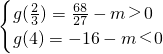
解得
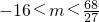
.(8分)
(Ⅲ)存在点P满足条件.(9分)
∵f(x)=x
3-6x
2+9x+3,
∴f'(x)=3x
2-12x+9=3(x-1)(x-3),
由f'(x)=0,得x
1=1,x
2=3.
当x<1时,f'(x)>0;当1<x<3时,f'(x)<0;当x>3时,f'(x)>0.
可知极值点为A(1,7),B(3,3),线段AB中点P(2,5)在曲线y=f(x)上,且该曲线关于点P(2,5)成中心对称.
证明如下:
∵f(x)=x
3-6x
2+9x+3,
∴f(4-x)=(4-x)
3-6(4-x)
2+9(4-x)+3=-x
3+6x
2-9x+7,
∴f(x)+f(4-x)=10.
上式表明,若点A(x,y)为曲线y=f(x)上任一点,其关于P(2,5)的对称点A(4-x,10-y)也在曲线y=f(x)上,曲线y=f(x)关于点P(2,5)对称.
故存在点P(2,5),使得过该点的直线若能与曲线y=f(x)围成两个封闭图形,这两个封闭图形的面积相等.…(12分)
分析:(Ⅰ)求得函数的导数,利用函数在某一点处导数的几何意义:f'(2)=-3以及f(2)=5,列方程组求解参数.
(Ⅱ)由(Ⅰ)中得到的函数解析式y=f(x)的图象与
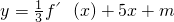
的图象有三个不同的交点,转化为方程
f(x)=
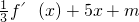
有三个不相等的实根,进一步转化为函数g(x)=f(x)-
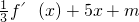
的图象与x轴有三个不同的交点,于是利用函数导数可得新函数g(x)的极值,通过判断极值的符号可得结论.
(Ⅲ)根据函数f(x)=x
3-6x
2+9x+3,可知极值点为A(1,7),B(3,3),进而证明线段AB中点P(2,5)在曲线y=f(x)上,且该曲线关于点P(2,5)成中心对称.
点评:本题考查函数的导数以及导数的几何意义,利用导数求解函数的单调性和极值问题,考查了函数的对称性,考查了函数与方程的思想,转化与化归的思想,综合性强.

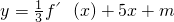 的图象有三个不同的交点,求实数m的取值范围;
的图象有三个不同的交点,求实数m的取值范围;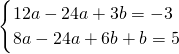 即
即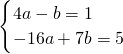
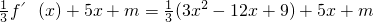 =x2+x+3+m,
=x2+x+3+m,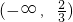

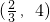
 ,极小值为g(4)=-16-m.(6分)
,极小值为g(4)=-16-m.(6分)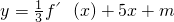 的图象有三个不同交点,则有:
的图象有三个不同交点,则有: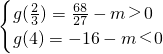
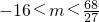 .(8分)
.(8分)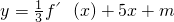 的图象有三个不同的交点,转化为方程
的图象有三个不同的交点,转化为方程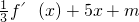 有三个不相等的实根,进一步转化为函数g(x)=f(x)-
有三个不相等的实根,进一步转化为函数g(x)=f(x)-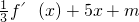 的图象与x轴有三个不同的交点,于是利用函数导数可得新函数g(x)的极值,通过判断极值的符号可得结论.
的图象与x轴有三个不同的交点,于是利用函数导数可得新函数g(x)的极值,通过判断极值的符号可得结论.
