
����Ŀ�����������Ǹ���ѧ�����ʵ�����һ����Ҫ���ݣ�����ij��ѧ�����ȡ��100��������100��Ů�����˽�����һ��μ����������ʱ�䣬��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ����λ��Сʱ������ͳ�ƣ��ó������μ���������ʱ���Ƶ�ʷֲ�����Ů���μ���������ʱ���Ƶ�ʷֲ�ֱ��ͼ.
����λ��Сʱ������ͳ�ƣ��ó������μ���������ʱ���Ƶ�ʷֲ�����Ů���μ���������ʱ���Ƶ�ʷֲ�ֱ��ͼ.
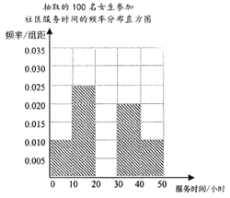
��1�����������μ���������ʱ���Ƶ�ʷֲ�����Ů���μ���������ʱ���Ƶ�ʷֲ�ֱ��ͼ.
��ȡ��100�������μ���������ʱ���Ƶ�ʷֲ���
��������ʱ�� | ���� | Ƶ�� |
| 0.05 | |
| 20 | |
| 0.35 | |
| 30 | |
| ||
�ϼ� | 100 | 1 |
ѧ����������ʱ��ϸ����Ա��������
���ϸ������ | �ϸ������ | |
�� | ||
Ů |
��2���������ۺ��������۵�Ҫ����ѧ��ÿ��μ����������ʱ�䲻����20��Сʱ��Ϊ�ϸ��������ͳ��ͼ������ɳ�ȡ����200��ѧ���μ���������ʱ��ϸ����Ա�������������ж��Ƿ���![]() ���ϵİ�����Ϊ�μ���������ʱ��ﵽ�ϸ�̶����Ա��йأ���˵������.
���ϵİ�����Ϊ�μ���������ʱ��ﵽ�ϸ�̶����Ա��йأ���˵������.
��3����������200��ѧ���μ����������ʱ�����ȫ��9��������ѧ���μ���������ʱ������������Ƶ����Ϊ����.
��i����ȫ�и���ѧ���μ���������ʱ�䲻����30��Сʱ������.
�����������и������μ���������������������.
�ο���ʽ
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.002 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
��![]() ����
����![]() ��
��
���𰸡���1����������2����������3��������
��������
��1�����ݹ�ʽ��ÿС���Ƶ�ʵ���ÿС���Ƶ����������������������⡣
������Ƶ�ʷֲ�ֱ��ͼ�У���С�����ε�������ܺ͵���1�������Ů����![]() ��С�����ε�������������Ƶ�ʷֲ�ֱ��ͼ��
��С�����ε�������������Ƶ�ʷֲ�ֱ��ͼ��
��2������ÿ��μ����������ʱ�䲻����20��Сʱ��Ϊ�ϸ���һҪ����100�������μ���������ʱ��Ƶ�ʷֲ�������������ϸ����������ϸ���������100��Ů���μ���������ʱ��Ƶ��ֱ��ͼ�У����Ů���ϸ����������ϸ���������д�����������![]() ,�ó����ۡ�
,�ó����ۡ�
��3����i������100�������μ���������ʱ��Ƶ�ʷֲ�����100��Ů���μ���������ʱ��Ƶ��ֱ��ͼ�����������200��ѧ���μ���������ʱ�䲻����30��Сʱ��������Ȼ�����ȫ�и�������������ʱ�䲻����30��Сʱ�ĸ��ʣ���������ȫ�и���ѧ���μ���������ʱ�䲻����30��Сʱ������.
���������Դ��������ĸ���������
Aȫ�и������Dz��Ƕ��ﵽ�����������۵�Ҫ���棻
Bȫ������ѧ���������������ʱ����ٷ��棻
Cȫ�и���ѧ���У�Ů���������������ʱ����������̷��棻
Dȫ�и���ѧ����������������ʱ��ij��̼����ĸ�ʱ��η��档
��1����ÿС���Ƶ�ʵ���ÿС���Ƶ���������������������ʽ���Լ����ÿһʱ���������д�����ݡ�
![]() ������=0.05
������=0.05![]() 100=5��
100=5��![]() �Σ�Ƶ��=20
�Σ�Ƶ��=20![]() 100=0.2��
100=0.2��
![]() ������=0.35
������=0.35![]() 100=35��
100=35�� ![]() �Σ�Ƶ��=30
�Σ�Ƶ��=30![]() 100=0.3��
100=0.3��
![]() ������=100
������=100![]() 5
5![]() 20
20![]() 35
35![]() 30=10��Ƶ��=1
30=10��Ƶ��=1![]() 0.05
0.05![]() 0.2
0.2![]() 0.35
0.35![]() 0.3=0.1��
0.3=0.1��
��ȫ��ȡ��100�������μ���������ʱ���Ƶ�ʷֲ��������±���
��������ʱ�� | ���� | Ƶ�� |
| 5 | 0.05 |
| 20 | 0.2 |
| 35 | 0.35 |
| 30 | 0.3 |
| 10 | 0.1 |
�ϼ� | 100 | 1 |
������Ƶ�ʷֲ�ֱ��ͼ�У���С�����ε�������ܺ͵���1��������
![]() ������Ƶ�ʷֲ�ֱ��ͼ����ͼ��
������Ƶ�ʷֲ�ֱ��ͼ����ͼ��
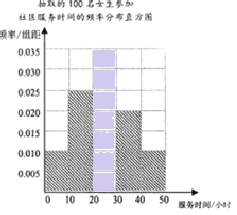
��2��ͨ����ȡ��100�������μ���������ʱ���Ƶ�ʷֲ�����֪�����ϸ�����Ϊ75�ˣ����ϸ�����Ϊ25�ˣ�ͨ����ȡ��100��Ů���μ���������ʱ��Ƶ��ֱ��ͼ�п�֪�ϸ�����Ϊ65�ˣ����ϸ�����Ϊ35�ˣ� ���������±���
ѧ����������ʱ��ϸ��������Ա��������
���ϸ������ | �ϸ������ | |
�� | 25 | 75 |
Ů | 35 | 65 |
![]() ��
��
��û��![]() ���ϰ�����Ϊ��������ʱ��ﵽ�ϸ����Ը��й�.
���ϰ�����Ϊ��������ʱ��ﵽ�ϸ����Ը��й�.
��3����i����ȡ����������������ʱ�䲻����30��Сʱ������Ϊ70�ˣ�Ƶ��Ϊ![]() ������ȫ�и�������������ʱ�䲻����30��Сʱ�ĸ���Ϊ
������ȫ�и�������������ʱ�䲻����30��Сʱ�ĸ���Ϊ![]() ������ȫ�и�������������ʱ�䲻����30��Сʱ������Ϊ
������ȫ�и�������������ʱ�䲻����30��Сʱ������Ϊ![]() ����.
����.
��ii���ɴ������ĸ��Ƕȷ�����Ҳ���Դ������Ƕȷ������Ƕ���ȷ�������������ɡ�
A�ӳ������ݿ��Եõ�ȫ�и���������һ����ѧ���������������ʱ��̫�٣����ܴﵽ�����������۵�Ҫ��
Bȫ������ѧ���������������ʱ�䶼ƫ�١�
Cȫ�и���ѧ���У�Ů���������������ʱ��������̡�
Dȫ�и���ѧ����������������ʱ��ij��̼�����![]() ֮��.
֮��.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����һ��ֱ��������ľ��![]() ����ƽ��ֱ������ϵ�У���֪
����ƽ��ֱ������ϵ�У���֪![]() ����
����![]() ��������ľ����һ�㣬����������ľ������Ӱ�����ܵ���Ҫ�����־�������þ�����
��������ľ����һ�㣬����������ľ������Ӱ�����ܵ���Ҫ�����־�������þ�����![]() ����һֱ��
����һֱ��![]() ��������ľ����
��������ľ����![]() .��ֱ��
.��ֱ��![]() ��б��Ϊ
��б��Ϊ![]() .
.
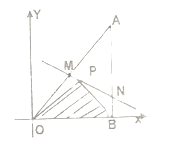
�������![]() �����꼰ֱ��
�����꼰ֱ��![]() ��б��
��б��![]() �ķ�Χ��
�ķ�Χ��
������![]() �����Ϊ
�����Ϊ![]() �������
�������![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
���������![]() ��ȡֵ��ΧΪ����
��ȡֵ��ΧΪ����![]() ����
����![]() ��
��![]() ���������
���������![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��
��![]() �Ķ���˵�Ϊ
�Ķ���˵�Ϊ![]() ��
��![]() ����
����![]() ����Բ
����Բ![]() �ϵĶ��㣬�Ҳ���
�ϵĶ��㣬�Ҳ���![]() ��
��![]() �غϣ���
�غϣ���![]() ����
����![]() ��
��![]() .
.
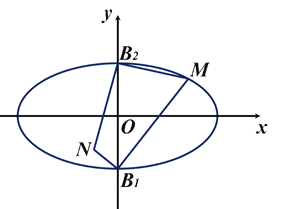
������![]() �Ĺ켣���̣�
�Ĺ켣���̣�
�������ı���![]() ��������ֵ.
��������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У�ֱ��
�У�ֱ��![]() ����б��Ϊ
����б��Ϊ![]() ���Ҿ�����
���Ҿ�����![]() ��������ԭ��OΪ���㣬x��������Ϊ���Ὠ��������ϵ��ֱ��
��������ԭ��OΪ���㣬x��������Ϊ���Ὠ��������ϵ��ֱ��![]() ����ԭ��O�����߽�
����ԭ��O�����߽�![]() �ڵ�M����NΪ����OM�ϵĵ㣬����
�ڵ�M����NΪ����OM�ϵĵ㣬����![]() ���ǵ�N�Ĺ켣Ϊ����C��
���ǵ�N�Ĺ켣Ϊ����C��
�������ֱ��![]() �IJ������̺�����C��ֱ�����귽�̣�
�IJ������̺�����C��ֱ�����귽�̣�
������ֱ��![]() ������C����P��Q���㣬��
������C����P��Q���㣬��![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() �Ķ���
�Ķ���![]() ��
��![]() ���ϵ��������ڵ�ֱ�߷�����
���ϵ��������ڵ�ֱ�߷�����![]() ��AC���ϵĸ����ڵ�ֱ�߷�����
��AC���ϵĸ����ڵ�ֱ�߷�����![]() ��
��
��1��AC�����ڵ�ֱ�߷��̣�
��2��AB�����ڵ�ֱ�߷��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ��
��![]() .
.
��1�����жϺ���![]() ��
��![]() �ϵĵ����ԣ���˵�����ɣ�
�ϵĵ����ԣ���˵�����ɣ�
��2����![]() ��������
��������![]() �ϵĵ�����������
�ϵĵ�����������![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ԲC����M��![]() ��1����N��
��1����N��![]() ��1�����㣬��Բ��C��ֱ��x+y��3��0�ϣ�����A����1��0���Ķ�ֱ��l��ԲC�ཻ��P��Q���㣮
��1�����㣬��Բ��C��ֱ��x+y��3��0�ϣ�����A����1��0���Ķ�ֱ��l��ԲC�ཻ��P��Q���㣮
������ԲC�ķ��̣�
����|PQ|��4![]() ʱ����ֱ��l�ķ��̣�
ʱ����ֱ��l�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Բ![]() �����ҽ���ֱ�Ϊ
�����ҽ���ֱ�Ϊ![]() ��
��![]() ���¶���Ϊ
���¶���Ϊ![]() ��
��![]() Ϊ����ԭ�㣬��
Ϊ����ԭ�㣬��![]() ��ֱ��
��ֱ��![]() �ľ���Ϊ
�ľ���Ϊ![]() ��
��![]() Ϊ����ֱ��������.
Ϊ����ֱ��������.
��1������Բ![]() �ı����̣�
�ı����̣�
��2��ֱ��![]() ����Բ
����Բ![]() ����
����![]() ��
��![]() ���㣬��ֱ��
���㣬��ֱ��![]() ��ֱ��
��ֱ��![]() ��б��֮��Ϊ
��б��֮��Ϊ![]() ��֤����ֱ��
��֤����ֱ��![]() ������㣬������ö��������.
������㣬������ö��������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��![]() ����Բ
����Բ![]() . ֱ��
. ֱ��![]() ����Բ
����Բ![]() ���ڲ�ͬ������
���ڲ�ͬ������![]() .
.
(��) ����Բ![]() �������ʣ�
�������ʣ�
(��) ��![]() ʱ����
ʱ����![]() �������
�������
������ֱ��![]() ����Բ
����Բ![]() ����һ������Ϊ
����һ������Ϊ![]() ����
����![]() Ϊ
Ϊ![]() �е�ʱ����
�е�ʱ����![]() ��ֵ .
��ֵ .
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com