
【题目】近年来,来自“一带一路”沿线的20国青年评选出了中国的“新四大发明”:高铁、扫码支付、共享单车和网购.其中共享单车既响应绿色出行号召,节能减排,保护环境,又方便人们短距离出行,增强灵活性.某城市试投放3个品牌的共享单车分别为红车、黄车、蓝车,三种车的计费标准均为每15分钟(不足15分钟按15分钟计)1元,按每日累计时长结算费用,例如某人某日共使用了24分钟,系统计时为30分钟.A同学统计了他1个月(按30天计)每天使用共享单车的时长如茎叶图所示,不考虑每月自然因素和社会因素的影响,用频率近似代替概率.设A同学每天消费![]() 元.
元.
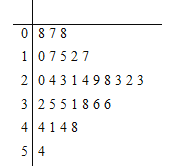
(1)求![]() 的分布列及数学期望;
的分布列及数学期望;
(2)各品牌为推广用户使用,推出APP注册会员的优惠活动:红车月功能使用费8元,每天消费打5折;黄车月功能使用费20元,每天前15分钟免费,之后消费打8折;蓝车月功能使用费45元,每月使用22小时之内免费,超出部分按每15分钟1元计费.设![]() 分别为红车,黄车,蓝车的月消费,写出
分别为红车,黄车,蓝车的月消费,写出![]() 与
与![]() 的函数关系式,参考(1)的结果,A同学下个月选择其中一个注册会员,他选哪个费用最低?
的函数关系式,参考(1)的结果,A同学下个月选择其中一个注册会员,他选哪个费用最低?
(3)该城市计划3个品牌的共享单车共3000辆正式投入使用,为节约居民开支,随机调查了100名用户一周的平均使用时长如下表:
时长 | (0,15] | (15,30] | (30,45] | (45,60] |
人数 | 16 | 45 | 34 | 5 |
在(2)的活动条件下,每个品牌各应该投放多少辆?
【答案】(1)分布列见解析,![]() (2)选红车(3)480,1500,1020
(2)选红车(3)480,1500,1020
【解析】
(1)根据茎叶图![]() 可能的取值有
可能的取值有![]() ,分别求出其分布列及期望即可;
,分别求出其分布列及期望即可;
(2)根据题意分别写出![]() 与
与![]() 的函数关系式,并算出A同学在每种优惠活动下的费用,看哪个费用最低即可;
的函数关系式,并算出A同学在每种优惠活动下的费用,看哪个费用最低即可;
(3)算出每个时长下每个品牌的费用,比较大小,确定每个时长下选择的最优惠的品牌,根据比例算出每个品牌各应该投放的辆数.
解:(1)根据茎叶图统计A同学30天里面每天使用共享单车的时长![]() 有6天,
有6天,![]() 有12天,
有12天,![]() 有10天,
有10天,![]() 有2天,
有2天,
则![]() 可能的取值有
可能的取值有![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
| 1 | 2 | 3 | 4 |
|
|
|
|
|
![]() ;
;
(2)红车![]() ,即
,即![]() ;
;
黄车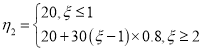 ,即
,即![]() ;
;
蓝车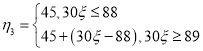 ,即
,即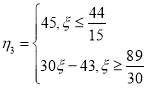 ;
;
若A同学下个月选择红车注册会员,则其消费为:![]() 元,
元,
若A同学下个月选择黄车注册会员,则其消费为:![]() 元,
元,
若A同学下个月选择蓝车注册会员,则其消费为:![]() 元,
元,
故选红车费用最低;
(3)当平均时长为(0,15]时,红车消费![]() 元,黄车消费
元,黄车消费![]() 元,蓝车消费
元,蓝车消费![]() 元,故此时选黄车;
元,故此时选黄车;
当平均时长为(15,30]时,红车消费![]() 元,黄车消费
元,黄车消费![]() 元,蓝车消费
元,蓝车消费![]() 元,故此时选红车;
元,故此时选红车;
当平均时长为(30,45]时,红车消费![]() 元,黄车消费
元,黄车消费![]() 元,蓝车消费
元,蓝车消费![]() 元,故此时选蓝车;
元,故此时选蓝车;
当时长为(45,60]时,红车消费![]() 元,黄车消费
元,黄车消费![]() 元,蓝车消费
元,蓝车消费![]() 元,故此时选红车;
元,故此时选红车;
故选红车的人数为50,选黄车的人数为16,选蓝车的人数为34,
故红车应该投放![]() 辆,黄车应该投放
辆,黄车应该投放![]() 辆,蓝车应该投放
辆,蓝车应该投放![]() 辆,
辆,
综合:红车应该投放![]() 辆,黄车应该投放
辆,黄车应该投放![]() 辆,蓝车应该投放
辆,蓝车应该投放![]() 辆.
辆.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,焦距为
,焦距为![]() .斜率为k的直线l与椭圆M有两个不同的交点A,B.
.斜率为k的直线l与椭圆M有两个不同的交点A,B.
(Ⅰ)求椭圆M的方程;
(Ⅱ)若![]() ,求
,求![]() 的最大值;
的最大值;
(Ⅲ)设![]() ,直线PA与椭圆M的另一个交点为C,直线PB与椭圆M的另一个交点为D.若C,D和点
,直线PA与椭圆M的另一个交点为C,直线PB与椭圆M的另一个交点为D.若C,D和点![]() 共线,求k.
共线,求k.
查看答案和解析>>
科目:高中数学 来源: 题型:
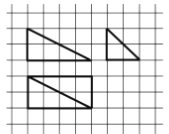
【题目】我国古代数学名著《九章算术·商功》中阐述:“斜解立方,得两壍堵。斜解壍堵,其一为阳马,一为鳖臑.阳马居二,鳖臑居一,不易之率也.合两鳖臑三而一,验之以棊,其形露矣.”若称为“阳马”的某几何体的三视图如图所示,图中网格纸上小正方形的边长为1,则对该几何体描述:
①四个侧面都是直角三角形;
②最长的侧棱长为![]() ;
;
③四个侧面中有三个侧面是全等的直角三角形;
④外接球的表面积为![]() .
.
其中正确的个数为( )
A. 0B. 1
C. 2D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知矩形![]() ,
,![]() ,
,![]() ,将
,将![]() 沿矩形的对角线
沿矩形的对角线![]() 所在的直线进行翻折,在翻折过程中,则( ).
所在的直线进行翻折,在翻折过程中,则( ).
A. 当![]() 时,存在某个位置,使得
时,存在某个位置,使得![]()
B. 当![]() 时,存在某个位置,使得
时,存在某个位置,使得![]()
C. 当![]() 时,存在某个位置,使得
时,存在某个位置,使得![]()
D. ![]() 时,都不存在某个位置,使得
时,都不存在某个位置,使得![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,函数
,函数![]() 且
且![]() .
.
(1)求p,q的值以及函数![]() 的表达式,并写出
的表达式,并写出![]() 的定义域D;
的定义域D;
(2)设函数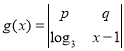 ,A=
,A=![]() ,集合
,集合![]() ,当
,当![]() 时,求实数k的取值范围;
时,求实数k的取值范围;
(3)当![]() 时,设
时,设![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,是否存在实数
,是否存在实数![]() ,使
,使![]() 对一切
对一切![]() 恒成立,若存在,分别求出实数
恒成立,若存在,分别求出实数![]() 的取值范围,若不存在,说明理由.
的取值范围,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,P是圆x2+y2=4上的动点,P点在x轴上的射影是D,点M满足![]() .
.

(Ⅰ)求动点M的轨迹C的方程
(Ⅱ)设A、B是轨迹C上的不同两点,点E(﹣4,0),且满足![]() ,若λ∈[
,若λ∈[![]() ,1),求直线AB的斜率k的取值范围.
,1),求直线AB的斜率k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四面体![]() 中,
中,![]() ,且
,且![]() 两两互相垂直,点
两两互相垂直,点![]() 是
是![]() 的中心.
的中心.

(1)求二面角![]() 的大小(用反三角函数表示);
的大小(用反三角函数表示);
(2)过![]() 作
作![]() ,垂足为
,垂足为![]() ,求
,求![]() 绕直线
绕直线![]() 旋转一周所形成的几何体的体积;
旋转一周所形成的几何体的体积;
(3)将![]() 绕直线
绕直线![]() 旋转一周,则在旋转过程中,直线
旋转一周,则在旋转过程中,直线![]() 与直线
与直线![]() 所成角记为
所成角记为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com