练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．设y=x+$\frac{1}{x-2}$（x＞2）．当x=a时，y有最小值，则a的值是（　　）
    A．4B．3C．1+$\sqrt{3}$D．1+$\sqrt{2}$

    分析 将原式变形y=x-2+$\frac{1}{x-2}$+2，由x-2＞0根据不等式的性质，y=x-2+$\frac{1}{x-2}$+2≥2$\sqrt{（x-2）×\frac{1}{x-2}}$=2=2+2=4，当x-2=$\frac{1}{x-2}$时取“=”，即可求得a的值．

    解答 解：y=x+$\frac{1}{x-2}$=x-2+$\frac{1}{x-2}$+2，
    ∵x＞2，
    ∴x-2＞0，
    ∴y=x-2+$\frac{1}{x-2}$+2≥2$\sqrt{（x-2）×\frac{1}{x-2}}$=2=2+2=4，
    ∴当x-2=$\frac{1}{x-2}$时取“=”，即x=3时取“=”
    ∴当x=3时，y有最小值4，
    ∴a=3，
    故答案选：B．

    点评 本题考查基本不等式的性质及应用，熟练掌握基本不等式的性质是解题的关键，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    2．已知数列{an}的前n项和为Sn，若an=$\frac{1}{\sqrt{n}+\sqrt{n-1}}$（n∈N*），则S2009的值为$\sqrt{2009}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知△ABC的面积是3，角A，B．C所对边长分别为a，b，c，cosA=$\frac{4}{5}$．
    （Ⅰ）求$\overrightarrow{AB}•\overrightarrow{AC}$；
    （Ⅱ）若b=2，求a的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．计算：（${lg\frac{1}{25}$-lg4）÷${100^{-\frac{1}{2}}}$的值为-20．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．已知cosθ=-$\frac{5}{13}$，θ∈（π，$\frac{3π}{2}$），则cos（θ-$\frac{π}{6}$）的值为-$\frac{5\sqrt{3}+12}{26}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．设X～B（n，p），且E（X）=12，D（X）=4，则n与p的值分别为（　　）
    A．18，$\frac{1}{3}$B．12，$\frac{2}{3}$C．18，$\frac{2}{3}$D．12，$\frac{1}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

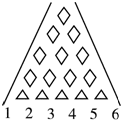    1．某个游戏中，一个珠子按如图所示的通道，由上至下的滑下，从最下面的六个出口出来，规定猜中者为胜，如果某人在该游戏中，猜得珠子从3号口出来，那么他取胜的概率为$\frac{5}{16}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．已知Ω是由曲线y=$\sqrt{4-{x}^{2}}$与x轴围成的封闭区域，若将质点P（x，y）投入区域Ω中，则x＞$\sqrt{3}$y的概率为（　　）
    A．$\frac{1}{6}$B．$\frac{1}{3}$C．$\frac{4}{3}$D．$\frac{2}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．已知角α的终边上一点P的坐标为（sin$\frac{2π}{3}$，cos$\frac{2π}{3}$），则sinα的值为（　　）
    A．$\frac{1}{2}$B．$-\frac{1}{2}$C．$\frac{{\sqrt{3}}}{2}$D．$-\frac{{\sqrt{3}}}{2}$

    查看答案和解析>>

    同步练习册答案