
【题目】为了研究某药品的疗效,选取若干名志愿者进行临床试验.所有志愿者的舒张压数据(单位:kPa)的分组区间为[12,13),[13,14),[14,15),[15,16),[16,17],将其按从左到右的顺序分别编号为第一组,第二组,…,第五组.如图是根据试验数据制成的频率分布直方图.已知第一组与第二组共有20人,第三组中没有疗效的有6人,则第三组中有疗效的人数为( ) 
A.6
B.8
C.12
D.18
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]()
(I)求函数在点(1,0)处的切线方程;
(II)设实数k使得f(x)< kx恒成立,求k的范围;
(III)设函数![]() ,求函数h(x)在区间
,求函数h(x)在区间![]() 上的零点个数.
上的零点个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴长为4,直线
的长轴长为4,直线![]() 被椭圆
被椭圆![]() 截得的线段长为
截得的线段长为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过椭圆![]() 的右顶点作互相垂直的两条直线
的右顶点作互相垂直的两条直线![]() 分别交椭圆
分别交椭圆![]() 于
于![]() 两点(点
两点(点![]() 不同于椭圆
不同于椭圆![]() 的右顶点),证明:直线
的右顶点),证明:直线![]() 过定点
过定点![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知矩形ABCD的边AB=2,BC=1,以A为坐标原点,AB,AD边分别在x轴、y轴的正半轴上,建立直角坐标系。将矩形折叠,使A点落在线段DC上,重新记为点![]()
(1)当点![]() 坐标为(1,1)时,求折痕所在直线方程.
坐标为(1,1)时,求折痕所在直线方程.
(2)若折痕所在直线的斜率为k,试求折痕所在直线的方程;
(3)当![]() 时,设折痕所在直线与
时,设折痕所在直线与![]() 轴交于点E,与
轴交于点E,与![]() 轴交于点F,将
轴交于点F,将![]() 沿折痕EF旋转.使二面角
沿折痕EF旋转.使二面角![]() 的大小为
的大小为![]() ,设三棱锥
,设三棱锥![]() 的外接球表面积为
的外接球表面积为![]() ,试求
,试求![]() 最小值.
最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是中国古代第一部数学专著,成于公元一世纪左右,系统总结了战国、秦、汉时期的数学成就.其中《方田》一章中记载了计算弧田(弧田就是由圆弧和其所对弦所围成弓形)的面积所用的经验公式:弧田面积=![]() (弦×矢+矢×矢),公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.按照上述经验公式计算所得弧田面积与其实际面积之间存在误差.现有圆心角为
(弦×矢+矢×矢),公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.按照上述经验公式计算所得弧田面积与其实际面积之间存在误差.现有圆心角为![]() ,弦长为
,弦长为![]() 的弧田.其实际面积与按照上述经验公式计算出弧田的面积之间的误差为( )平方米.(其中
的弧田.其实际面积与按照上述经验公式计算出弧田的面积之间的误差为( )平方米.(其中![]() ,
,![]() )
)
A. 15 B. 16 C. 17 D. 18
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的公差为2,前n项和为Sn , 且S1 , S2 , S4成等比数列.
(1)求数列{an}的通项公式;
(2)令bn=(﹣1)n﹣1 ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数y=3sin(2x+ ![]() )的图象向右平移
)的图象向右平移 ![]() 个单位长度,所得图象对应的函数( )
个单位长度,所得图象对应的函数( )
A.在区间[ ![]() ,
, ![]() ]上单调递减
]上单调递减
B.在区间[ ![]() ,
, ![]() ]上单调递增
]上单调递增
C.在区间[﹣ ![]() ,
, ![]() ]上单调递减
]上单调递减
D.在区间[﹣ ![]() ,
, ![]() ]上单调递增
]上单调递增
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】教材上一例问题如下:
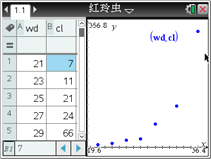
一只红铃虫的产卵数y和温度x有关,现收集了7组观测数据如下表,试建立y与x之间的回归方程.
温度 x/℃ | 21 | 23 | 25 | 27 | 29 | 32 | 35 |
产卵数y/个 | 7 | 11 | 21 | 24 | 66 | 115 | 325 |
某同学利用图形计算器研究它时,先作出散点图(如图所示),发现两个变量不呈线性相关关系. 根据已有的函数知识,发现样本点分布在某一条指数型曲线![]() 的附近(
的附近(![]() 和
和![]() 是待定的参数),于是进行了如下的计算:
是待定的参数),于是进行了如下的计算:
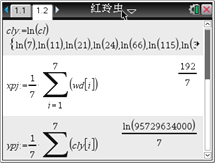
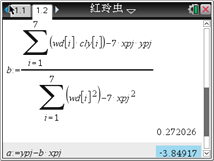
根据以上计算结果,可以得到红铃虫的产卵数y对温度x的回归方程为__________.(精确到0.0001) (提示:![]() 利用代换可转化为线性关系)
利用代换可转化为线性关系)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com