
����Ŀ��ij�̳�����һ������Ϊÿ��30Ԫ����Ʒ�����г������з���������Ʒ�����۵���x(Ԫ)����������y(��)֮�������±���ʾ�Ĺ�ϵ��
x | 30 | 40 | 45 | 50 |
y | 60 | 30 | 15 | 0 |
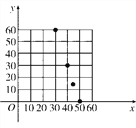
������������ͼֽ�У����ݱ����ṩ�����ݣ����ʵ����(x��y)�Ķ�Ӧ�㣬��ȷ��y��x��һ��������ϵʽ��

(2)�辭Ӫ����Ʒ������������ΪPԪ������������ϵ��д��P����x�ĺ�����ϵʽ����ָ�����۵���xΪ����Ԫʱ�����ܻ���������������
���𰸡�(1) y����3x��150(0��x��50��x��N*)�� (2) P����3(x��40)2��300�����۵���Ϊ40Ԫʱ�����ܻ���������������
�������������������1�������⻭�������ĵ㣬����������һ�κ����Ľ���ʽ���ɣ�
��2����ϣ�1���Ľ��ۺͶ��κ����������������㼴��������ս����
���������
(1)�ɱ�������(30��60)��(40��30)��(45��15)��(50��0).��ͼ�����ǽ��Ƶ���һ��ֱ���ϣ������ǹ�����ֱ��y��kx��b��
��![]() ���
���![]()
��y����3x��150��(x��N).
������(30��60)��(40��30)Ҳ�ڴ�ֱ����.
������������ʽΪy����3x��150��(x��N).
(2)������P��y(x��30)��(��3x��150)(x��30)����3(x��40)2��300��
��x��40ʱ��P�����ֵ300�������ۼ�Ϊ40Ԫʱ�����ܻ���������.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���ɼס�������ƹ������ֲ��������豸�ͷ��ܺã����շѷ�ʽ��ͬ����ÿ����̨ÿСʱ5Ԫ���ҼҰ��¼Ʒѣ�һ������![]() Сʱ���ڣ���
Сʱ���ڣ���![]() Сʱ��ÿ����̨
Сʱ��ÿ����̨![]() Ԫ������
Ԫ������![]() Сʱ�IJ���ÿ����̨ÿСʱ
Сʱ�IJ���ÿ����̨ÿСʱ![]() Ԫ.ij��˾���¸��´������е�һ����һ����̨��չ����ʱ�䲻����
Ԫ.ij��˾���¸��´������е�һ����һ����̨��չ����ʱ�䲻����![]() Сʱ��Ҳ������
Сʱ��Ҳ������![]() Сʱ�����ڼ���һ����̨��չ�
Сʱ�����ڼ���һ����̨��չ�![]() Сʱ���շ�Ϊ
Сʱ���շ�Ϊ![]() Ԫ�����Ҽ���һ����̨��չ�
Ԫ�����Ҽ���һ����̨��չ�![]() Сʱ���շ�Ϊ
Сʱ���շ�Ϊ![]() Ԫ.
Ԫ.
��1���Էֱ�д��![]() ��
��![]() �Ľ���ʽ��
�Ľ���ʽ��
��2��ѡ���ļұȽϺ��㣿��˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��������
��������![]() ����ͼ����x��Ľ����У�������������֮��ľ���Ϊ
����ͼ����x��Ľ����У�������������֮��ľ���Ϊ![]() ����ͼ����һ����͵�Ϊ
����ͼ����һ����͵�Ϊ![]() ��
��
������![]() �Ľ���ʽ��
�Ľ���ʽ��
����![]() ����
����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Բ![]() :
:![]() ��ֱ��
��ֱ��![]() ��
�� ![]() ��
��
��1�����![]() ��ֱ��
��ֱ��![]() �ϵ�һ���㣬��
�ϵ�һ���㣬��![]() ����Բ
����Բ![]() ���������ߣ��е�ֱ�Ϊ
���������ߣ��е�ֱ�Ϊ![]() �����ı���
�����ı���![]() ���������Сֵ��
���������Сֵ��
��2����![]() ��ֱ��
��ֱ��![]() �Ĵ��߽�Բ
�Ĵ��߽�Բ![]() ��
��![]() �㣬
�㣬 ![]() Ϊ
Ϊ![]() ����
����![]() ��ĶԳƵ㣬��
��ĶԳƵ㣬��![]() ��Բ
��Բ![]() ������
������![]() ��������ͬ�㣬�����㣺
��������ͬ�㣬�����㣺 ![]() ����֤��ֱ��
����֤��ֱ��![]() ��б��Ϊ��ֵ��
��б��Ϊ��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������������Ƚ��ۣ�
������ ![]() ����|
����| ![]() |2=
|2= ![]() 2����ȸ���z����|z|2=z2
2����ȸ���z����|z|2=z2
��ʵ��a��b�У�a+b��2=a2+2ab+b2��������� ![]() ��
�� ![]() ����
���� ![]() ��2=
��2= ![]() 2
2 ![]() 2
2
��ʵ��a��b��a2+b2=0����a=b=0����ȸ���z1 �� z2 �� ��z12+z22=0����z1=z2=0
������Ƚ�����ȷ���������Ϊ�� ��
A.0
B.1
C.2
D.3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=��2x+b��ex �� F��x��=bx��lnx��b��R��
��1����b��0���Ҵ�������M��ʹf��x����F��x��������M�Ͼ�����ͬ�ĵ����ԣ���b��ȡֵ��Χ��
��2����F��x+1����b������x�ʣ�0��+�ޣ����������b��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ��
�� ![]() .
.
��1����![]() �Ľ���ʽ��
�Ľ���ʽ��
��2����![]() ��ֵ��
��ֵ��
��3����![]() ��
�� ![]() ʱ��������
ʱ��������![]() ����
����![]() ��������
��������![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��={��x��y��|0��x��1��0��y��1}��A����ֱ��y=0��x=a��0��a��1��������y=x3Χ�ɵ����������ε�ƽ�������������������Ͷһ��P����P��������A�ڵĸ����� ![]() ����a��ֵΪ�� ��
����a��ֵΪ�� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com