解:(1)由题意:

,∴a+3b=0…①
又g′(x)=-2x+1,∴g(x)的图象在点P切线的斜率为:g′(1)=-1
又f′(x)=ax
2+2bx+2,∴f(x)的图象在点P切线的斜率为:f′(1)=a+2b+2=1…②
由①②可解得:a=-3,b=1,∴f(x)=-x
3+x
2+2x-1,…(3分)
∴h(x)=f(x)-x=-x
3+x
2+x-1,∴h′(x)=-3x
2+2x+1=(3x+1)(-x+1)
令h′(x)=(3x+1)(-x+1)≥0,解得:

即函数h(x)的单调递增区间为:

.…(6分)
(2)对任意x
1,x
2∈[-1,1],f(x
1)+k<g(x
2)恒成立?当x
1,x
2∈[-1,1]时,f(x
1)
max+k<g(x
2)
min成立…(★) …(8分)
∵f′(x)=-3x
2+2x+2,x∈[-1,1],令f′(x)>0,解得:

∴f(x)区间

上递减,在区间

上递增
又f(-1)=-1,f(1)=1,
∴当x∈[-1,1]时,f(x)
max=f(1)=1…(10分)
而

,
∴当x∈[-1,1]时,g(x)
min=g(-1)=-1
∴由(★)式有:1+k<-1,
∴实数k的取值范围为:(-∞,-2).…(12分)
分析:(1)根据函数f(x)与g(x)的图象的一个交点P的横坐标为1,且两曲线在点P处的切线互相垂直.求出f(x)=-x
3+x
2+2x-1,再利用导数法求函数的单调递增区间.
(2)对任意x
1,x
2∈[-1,1],f(x
1)+k<g(x
2)恒成立?当x
1,x
2∈[-1,1]时,f(x
1)
max+k<g(x
2)
min成立,利用导数法,可求最值,从而得解.
点评:本题以函数为载体,考查函数的解析式,考查函数的单调性,考查恒成立问题的处理,注意利用导数求函数的最值.

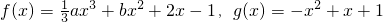 ,若函数f(x)与g(x)的图象的一个交点P的横坐标为1,且两曲线在点P处的切线互相垂直.
,若函数f(x)与g(x)的图象的一个交点P的横坐标为1,且两曲线在点P处的切线互相垂直. ,∴a+3b=0…①
,∴a+3b=0…①
 .…(6分)
.…(6分)
 上递减,在区间
上递减,在区间 上递增
上递增 ,
,

 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案