
【题目】已知函数f(x)=loga ![]() (a>0,a≠1).
(a>0,a≠1).
(1)当a>1时,讨论f(x)的奇偶性,并证明函数f(x)在(1,+∞)上为单调递减;
(2)当x∈(n,a﹣2)时,是否存在实数a和n,使得函数f(x)的值域为(1,+∞),若存在,求出实数a与n的值,若不存在,说明理由.
【答案】
(1)解:f(x)的定义域为{x|x<﹣1或x>1},关于原点对称,
又f(﹣x)= ![]() ,∴f(x)为奇函数,
,∴f(x)为奇函数,
证明:当a>1时,设1<x1<x2,则
f(x1)﹣f(x2)= ![]() =
= ![]() ,
,
∵ ![]() =
= ![]() ,
,
∴ ![]() >1,又a>1,∴loga
>1,又a>1,∴loga ![]() >0,则f(x1)>f(x2),
>0,则f(x1)>f(x2),
∴函数f(x)在(1,+∞)上为减函数
(2)解:令 ![]() =
= ![]() ,x∈(n,a﹣2),
,x∈(n,a﹣2),
①当a>1时,要使f(x)的值域为(1,+∞),则须t∈(a,+∞),
令 ![]() ,解得
,解得 ![]() .∴x∈(1,
.∴x∈(1, ![]() ).
).
故有 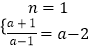 ,解得
,解得 ![]() ;
;
②当0<a<1时,t∈(0,a),则x∈( ![]() ),∴
),∴ 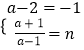 ,(不合题意).
,(不合题意).
综上所述,存在实数n=1,a= ![]() ,当x∈(n,a﹣2)时,函数f(x)的值域为(1,+∞)
,当x∈(n,a﹣2)时,函数f(x)的值域为(1,+∞)
【解析】(1)直接利用函数单调性与奇偶性的定义判断;(2)令 ![]() =
= ![]() ,x∈(n,a﹣2),当a>1时,要使f(x)的值域为(1,+∞),则须t∈(a,+∞),令
,x∈(n,a﹣2),当a>1时,要使f(x)的值域为(1,+∞),则须t∈(a,+∞),令 ![]() ,解得
,解得 ![]() .可得x∈(1,
.可得x∈(1, ![]() ).则
).则 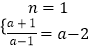 ,解得
,解得 ![]() ;当0<a<1时,t∈(0,a),则x∈(
;当0<a<1时,t∈(0,a),则x∈( ![]() ),得
),得 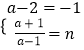 ,(不合题意).由此可得存在实数n=1,a=
,(不合题意).由此可得存在实数n=1,a= ![]() ,当x∈(n,a﹣2)时,函数f(x)的值域为(1,+∞).
,当x∈(n,a﹣2)时,函数f(x)的值域为(1,+∞).
【考点精析】掌握奇偶性与单调性的综合是解答本题的根本,需要知道奇函数在关于原点对称的区间上有相同的单调性;偶函数在关于原点对称的区间上有相反的单调性.


科目:高中数学 来源: 题型:
【题目】(文)已知y=f(x)是偶函数,y=g(x)是奇函数,它们的定义域均为[﹣3,3],且它们在x∈[0,3]上的图象如图所示,则不等式 ![]() 的解集是
的解集是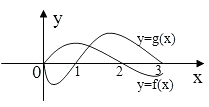
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知an=logn+1(n+2)(n∈N+),观察下列运算:a1a2=log23log34= ![]() =2;a1a2a3a4a5a6=log23log34…log67lg78=
=2;a1a2a3a4a5a6=log23log34…log67lg78= ![]() =3;….定义使a1a2a3…ak为整数的k(k∈N+)叫做希望数,则在区间[1,2016]内所有希望数的和为( )
=3;….定义使a1a2a3…ak为整数的k(k∈N+)叫做希望数,则在区间[1,2016]内所有希望数的和为( )
A.1004
B.2026
C.4072
D.22016﹣2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为方便市民休闲观光,市政府计划在半径为200米,圆心角为120°的扇形广场内(如图所示),沿△ABC边界修建观光道路,其中A、B分别在线段CP、CQ上,且A、B两点间距离为定长 ![]() 米.
米. 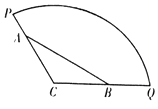
(1)当∠BAC=45°时,求观光道BC段的长度;
(2)为提高观光效果,应尽量增加观光道路总长度,试确定图中A、B两点的位置,使观光道路总长度达到最长?并求出总长度的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明同学在寒假社会实践活动中,对白天平均气温与某家奶茶店的![]() 品牌饮料销量之间的关系进行了分析研究,他分别记录了1月11日至1月15日的白天气温
品牌饮料销量之间的关系进行了分析研究,他分别记录了1月11日至1月15日的白天气温![]() (
(![]() )与该奶茶店的
)与该奶茶店的![]() 品牌饮料销量
品牌饮料销量![]() (杯),得到如表数据:
(杯),得到如表数据:
日期 | 1月11号 | 1月12号 | 1月13号 | 1月14号 | 1月15号 |
平均气温 | 9 | 10 | 12 | 11 | 8 |
销量 | 23 | 25 | 30 | 26 | 21 |
(1)若先从这五组数据中抽出2组,求抽出的2组数据恰好是相邻2天数据的概率;
(2)请根据所给五组数据,求出![]() 关于
关于![]() 的线性回归方程式
的线性回归方程式![]() ;
;
(3)根据(2)所得的线性回归方程,若天气预报1月16号的白天平均气温为![]() ,请预测该奶茶店这种饮料的销量.
,请预测该奶茶店这种饮料的销量.
(参考公式: ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为常数,
为常数, ![]() 是自然对数的底数),曲线
是自然对数的底数),曲线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴平行.
轴平行.
(1)求![]() 的值;
的值;
(2)求![]() 的单调区间;
的单调区间;
(3)设![]() ,其中
,其中![]() 为
为![]() 的导函数.证明:对任意
的导函数.证明:对任意![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,已知中心在原点,离心率为
中,已知中心在原点,离心率为![]() 的椭圆
的椭圆![]() 的一个焦点为圆
的一个焦点为圆![]() :
: ![]() 的圆心.
的圆心.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设![]() 是椭圆
是椭圆![]() 上一点,过
上一点,过![]() 作两条斜率之积为
作两条斜率之积为![]() 的直线
的直线![]() ,
, ![]() ,当直线
,当直线![]() ,
, ![]() 都与圆
都与圆![]() 相切时,求
相切时,求![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com