
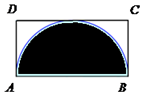
 若将一个质点随机投入如图所示的长方形ABCD中,其中AB=2,BC=1,则质点落在以AB为直径的半圆内的概率是( )
若将一个质点随机投入如图所示的长方形ABCD中,其中AB=2,BC=1,则质点落在以AB为直径的半圆内的概率是( )| A. | $\frac{π}{8}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{5}$ | D. | $\frac{π}{2}$ |
 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
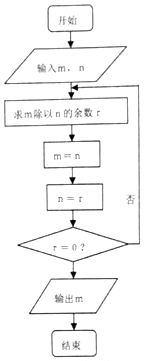 如图程序框图的算法思路源于欧几里得名著《几何原本》中的“辗转相除法”,执行该程序框图,若输入m,n分别为225、135,则输出的m=( )
如图程序框图的算法思路源于欧几里得名著《几何原本》中的“辗转相除法”,执行该程序框图,若输入m,n分别为225、135,则输出的m=( )| A. | 5 | B. | 9 | C. | 45 | D. | 90 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
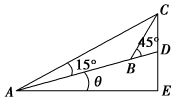 如图所示,在坡度一定的山坡A处测得山顶上一建筑物CD的顶端C对于山坡的斜度为15°,向山顶前进100m到达B处,又测得C对于山坡的斜度为45°,若CD=50m,山坡对于地平面的坡度为θ,则cosθ=$\sqrt{3}$-1.
如图所示,在坡度一定的山坡A处测得山顶上一建筑物CD的顶端C对于山坡的斜度为15°,向山顶前进100m到达B处,又测得C对于山坡的斜度为45°,若CD=50m,山坡对于地平面的坡度为θ,则cosθ=$\sqrt{3}$-1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 手工社 | 摄影社 | 总计 | |
| 女生 | 6 | ||
| 男生 | 42 | ||
| 总计 | 30 | 60 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1024 | B. | 1023 | C. | 2048 | D. | 2046 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com