
分析 (1)由题意可得等差数列{an}的公差d,可得通项公式;
(2)由(1)可得Sn,由二次函数的知识可得.
解答 解:(1)设等差数列{an}的公差为d,
由题意可得a7-a3=4d=-4-(-12)=8,解得d=2.
∴an=a3+(n-3)d=-12+2(n-3)=2n-18,
∴数列{an}的通项公式为an=2n-18;
(2)由(1)可得an=2n-18,
∴${S_n}=\frac{{n({a_1}+{a_n})}}{2}=\frac{n[-16+(2n-18)]}{2}={n^2}-17n$.
由二次函数和n∈N*可得当n=8或n=9时,Sn取得最小值为S8=S9=-72.
故数列{an}的前n项和${S_n}={n^2}-17n$,Sn的最小值为-72
点评 本题考查等差数列的求和公式,涉及二次函数的最值,属基础题.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案科目:高中数学 来源: 题型:选择题
| A. | ?x>0,2x>x2 | B. | ?x0∈R,e${\;}^{{x}_{0}}$≤0 | ||
| C. | “a>b“是“ac2>bc2”的充要条件 | D. | “ab>1”是“a>1,b>1”的必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | an+an+3>an+1+an+2 | B. | an+an+3=an+1+an+2 | ||
| C. | an+an+3<an+1+an+2 | D. | 与公比q有关 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30°或150° | B. | 60° | C. | 60°或120° | D. | 30° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a+b=2c | B. | a+b≤2c | C. | a+b<2c | D. | a+b≥2c |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 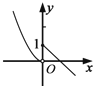 | B. | 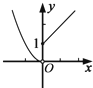 | C. | 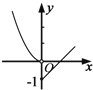 | D. | 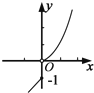 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com