
分析 由于焦点为F1(0,-1),F2(0,1),可设椭圆方程为$\frac{{y}^{2}}{{a}^{2}}+\frac{{x}^{2}}{{a}^{2}-1}$=1,把点P($\frac{\sqrt{2}}{2}$,1)代入即可.
解答 解:∵焦点为F1(0,-1),F2(0,1),∴可设椭圆方程为$\frac{{y}^{2}}{{a}^{2}}+\frac{{x}^{2}}{{a}^{2}-1}$=1;
∵点P($\frac{\sqrt{2}}{2}$,1)在椭圆上,∴$\frac{1}{{a}^{2}}+\frac{\frac{1}{2}}{{a}^{2}-1}$=1,解得a2=2,
∴椭圆方程为$\frac{{y}^{2}}{2}+{x}^{2}=1$.
故答案为:$\frac{{y}^{2}}{2}+{x}^{2}=1$.
点评 熟练掌握椭圆的标准方程及其性质是解题的关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
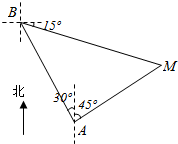 如图,一艘轮船按照北偏西30°的方向以每小时30海里的速度从A处开始航行,此时灯塔M在轮船的北偏东45°方向上,经过40分钟后,轮船到达B处,灯塔在轮船的东偏南15°方向上,则灯塔M和轮船起始位置A的距离为$\frac{20\sqrt{6}}{3}$海里.
如图,一艘轮船按照北偏西30°的方向以每小时30海里的速度从A处开始航行,此时灯塔M在轮船的北偏东45°方向上,经过40分钟后,轮船到达B处,灯塔在轮船的东偏南15°方向上,则灯塔M和轮船起始位置A的距离为$\frac{20\sqrt{6}}{3}$海里.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=3 | B. | x=2 | C. | x=2或3x-4y+6=0 | D. | 3x-4y+6=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1<a<$\frac{1}{3}$ | B. | a<$\frac{1}{3}$ | C. | a>$\root{3}{3}$ | D. | $\frac{1}{3}$<a<$\root{3}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com