
【题目】连续抛掷同一颗骰子3次,则3次掷得的点数之和为9的概率是____.
【答案】![]() ;
;
【解析】
利用分步计数原理,连续拋掷同一颗骰子3次,则总共有:6×6×6=216种情况,再列出满足条件的所有基本事件,利用古典概型的计算公式计算可得概率.
每一次拋掷骰子都有1,2,3,4,5,6,六种情况,
由分步计数原理:连续抛掷同一颗骰子3次,则总共有:6×6×6=216种情况,
则3次掷得的点数之和为9的基本事件为25种情况即:
(1,2,6),(1,3,5),(1,4,4),(1,5,3),(1,6,2),
(2,1,6),(2,2,5),(2,3,4),(2,4,3),(2,5,2),(2,6,1),
(3,1,5),(3,2,4),(3,3,3),(3,4,2),(3,5,1),
(4,1,4),(4,2,3),(4,3,2),(4,4,1),
(5,1,3),(5,2,2),(5,3,1),
(6,1,2),(6,2,1),共25个基本事件,所以![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,![]() 垂直于
垂直于![]() 所在的平面
所在的平面![]() ,
,![]() 为
为![]() 的直径,
的直径,![]() 是弧
是弧![]() 上的一个动点(不与端点
上的一个动点(不与端点![]() 重合),
重合),![]() 为
为![]() 上一点,且
上一点,且![]() 是线段
是线段![]() 上的一个动点(不与端点
上的一个动点(不与端点![]() 重合).
重合).

(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() 是弧
是弧![]() 的中点,
的中点,![]() 是锐角,且三棱锥
是锐角,且三棱锥![]() 的体积为
的体积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将一枚质地均匀的硬币连掷![]() 次,设事件
次,设事件![]() “恰好两次正面朝上”,
“恰好两次正面朝上”,
(1)直接计算事件![]() 的概率;
的概率;
(2)利用计算器或计算机模拟试验80次,计算事件![]() 发生的频率.
发生的频率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知点![]() 在椭圆
在椭圆![]() 上,将射线
上,将射线![]() 绕原点
绕原点![]() 逆时针旋转
逆时针旋转![]() ,所得射线
,所得射线![]() 交直线
交直线![]() 于点
于点![]() .以
.以![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求椭圆![]() 和直线
和直线![]() 的极坐标方程;
的极坐标方程;
(2)证明::![]() 中,斜边
中,斜边![]() 上的高
上的高![]() 为定值,并求该定值.
为定值,并求该定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了保障全国第四次经济普查顺利进行,国家统计局从东部选择江苏,从中部选择河北. 湖北,从西部选择宁夏,从直辖市中选择重庆作为国家综合试点地区,然后再逐级确定普查区域,直到基层的普查小区.在普查过程中首先要进行宣传培训,然后确定对象,最后入户登记.由于种种情况可能会导致入户登记不够顺利,这为正式普查提供了宝贵的试点经验.在某普查小区,共有 50 家企事业单位,150 家个体经营户,普查情况如下表所示:
普查对象类别 | 顺利 | 不顺利 | 合计 |
企事业单位 | 40 | 50 | |
个体经营户 | 50 | 150 | |
合计 |
(1)写出选择 5 个国家综合试点地区采用的抽样方法;
(2)补全上述列联表(在答题卡填写),并根据列联表判断是否有![]() 的把握认为“此普查小区的入户登记是否顺利与普查对象的类别有关”;
的把握认为“此普查小区的入户登记是否顺利与普查对象的类别有关”;
(3)根据该试点普查小区的情况,为保障第四次经济普查的顺利进行,请你从统计的角度提出一条建议.
附:![]()
| 0.10 | 0.010 | 0.001 |
| 2.706 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】华中师大附中中科教处为了研究高一学生对物理和数学的学习是否与性别有关,从高一年级抽取60,名同学(男同学30名,女同学30名),给所有同学物理题和数学题各一题,让每位同学自由选择一道题进行解答.选题情况如下表:(单位:人)

(1)在犯错误的概率不超过1%是条件下,能否判断高一学生对物理和数学的学习与性别有关?
(2)经过多次测试后发现,甲每次解答一道物理题所用的时间5—8分钟,乙每次解答一道物理题所用的时间为6—8分钟,现甲、乙解同一道物理题,求甲比乙先解答完的概率;
(3)现从选择做物理题的8名女生中任意选取两人,对题目的解答情况进行全程研究,记甲、乙两女生被抽到的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是R上的偶函数,对于
是R上的偶函数,对于![]() 都有
都有![]() 成立,且
成立,且![]() ,当
,当![]() ,且
,且![]() 时,都有
时,都有![]() .则给出下列命题:
.则给出下列命题:
①![]() ;
;
②函数![]() 图象的一条对称轴为
图象的一条对称轴为![]() ;
;
③函数![]() 在[﹣9,﹣6]上为减函数;④方程
在[﹣9,﹣6]上为减函数;④方程![]() 在[﹣9,9]上有4个根;
在[﹣9,9]上有4个根;
其中正确的命题序号是___________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,分别过椭圆![]() 左、右焦点
左、右焦点![]() 的动直线
的动直线![]() 相交于
相交于![]() 点,与椭圆
点,与椭圆![]() 分别交于
分别交于![]() 与
与![]() 不同四点,直线
不同四点,直线![]() 的斜率
的斜率![]() 满足
满足![]() , 已知
, 已知![]() 与
与![]() 轴重合时,
轴重合时, ![]() .
.
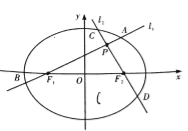
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在定点![]() 使得
使得![]() 为定值,若存在,求出
为定值,若存在,求出![]() 点坐标并求出此定值,若不存在,
点坐标并求出此定值,若不存在,
说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com