Question

16．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$，点A，B，F分别为椭圆C的左顶点、上顶点、左焦点，若∠AFB=∠BAF+90°，则椭圆C的离心率是$\frac{\sqrt{5}-1}{2}$．

Answer 1

分析 由题意画出图形，结合已知可得a，b，c的关系，进一步结合隐含条件可得关于离心率e的方程求解．

解答 解：如图，tan∠BAF=$\frac{b}{a}$，tan∠BFO=$\frac{b}{c}$，
∵∠AFB=∠BAF+90°，
∴∠BFO=180°-∠AFB=90°-∠BAF，
即tan∠BFO=$\frac{1}{tan∠BAF}$，
∴$\frac{b}{c}$=$\frac{a}{b}$，则b²=a²-c²=ac，由e=$\frac{c}{a}$，
∴e²+e-1=0，由0＜e＜1，
解得：e=$\frac{\sqrt{5}-1}{2}$，
故答案为：$\frac{\sqrt{5}-1}{2}$．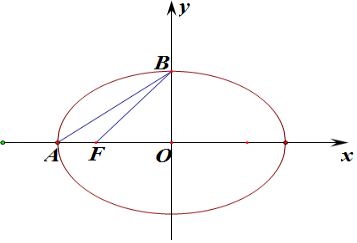

点评 本题考查椭圆的简单性质，考查了数形结合的解题思想方法，属于中档题．