
【题目】如图:在五面体![]() 中,四边形
中,四边形![]() 是正方形,
是正方形, ![]() ,
,
(1)证明:![]() 为直角三角形;
为直角三角形;
(2)已知四边形![]() 是等腰梯形,且
是等腰梯形,且![]() ,
,![]() ,求五面体
,求五面体![]() 的体积.
的体积.

 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 是椭圆
是椭圆![]() :
:![]() (
(![]() )与抛物线
)与抛物线![]() :
:![]() 的一个公共点,且椭圆与抛物线具有一个相同的焦点
的一个公共点,且椭圆与抛物线具有一个相同的焦点![]() .
.
(Ⅰ)求椭圆![]() 及抛物线
及抛物线![]() 的方程;
的方程;
(Ⅱ)设过![]() 且互相垂直的两动直线
且互相垂直的两动直线![]() ,
,![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,
两点,![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,求四边形
两点,求四边形![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为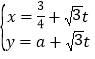 ,(
,(![]() 为参数),圆
为参数),圆![]() 的标准方程为
的标准方程为![]() .以坐标原点为极点,
.以坐标原点为极点, ![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求直线![]() 和圆
和圆![]() 的极坐标方程;
的极坐标方程;
(2)若射线![]() 与的交点为
与的交点为![]() ,与圆
,与圆![]() 的交点为
的交点为![]() ,且点
,且点![]() 恰好为线段
恰好为线段![]() 的中点,求
的中点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,离心率
,离心率![]() ,且椭圆的短轴长为2.
,且椭圆的短轴长为2.
(1)球椭圆的标准方程;
(2)已知直线![]() 过右焦点
过右焦点![]() ,且它们的斜率乘积为
,且它们的斜率乘积为![]() ,设
,设![]() 分别与椭圆交于点
分别与椭圆交于点![]() 和
和![]() .
.
①求![]() 的值;
的值;
②设![]() 的中点
的中点![]() ,
,![]() 的中点为,求
的中点为,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一种鱼的身体吸收汞,一定量身体中汞的含量超过其体重的1.00ppm(即百万分之一)的鱼被人食用后,就会对人体产生危害.在30条鱼的样本中发现的汞含量(单位:ppm)如下:
0.07 0.24 0.95 0.98 1.02 0.98 1.37 1.40 0.39 1.02
1.44 1.58 0.54 1.08 0.61 0.72 1.20 1.14 1.62 1.68
1.85 1.20 0.81 0.82 0.84 1.29 1.26 2.10 0.91 1.31
(1)请用合适的统计图描述上述数据,并分析这30条鱼的汞含量的分布特点;
(2)求出上述样本数据的平均数和标准差;
(3)从实际情况看,许多鱼的汞含量超标的原因是这些鱼在出售之前没有被检测过你认为每批这种鱼的平均承含量都比1.00ppm大吗?
(4)在上述样本中,有多少条鱼的汞含量在以平均数为中心、2倍标准差的范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,圆![]() 经过伸缩变换
经过伸缩变换![]() 后得到曲线
后得到曲线![]() .以坐标原点为极点,
.以坐标原点为极点,![]() 轴的正半轴为极轴,并在两种坐标系中取相同的单位长度,建立极坐标系,直线
轴的正半轴为极轴,并在两种坐标系中取相同的单位长度,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程及直线
的直角坐标方程及直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 是
是![]() 上一动点,求点
上一动点,求点![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com