
| 甲 | 27 | 38 | 30 | 37 | 35 | 31 |
| 乙 | 33 | 29 | 38 | 34 | 28 | 36 |
分析 (1)由已知画茎叶图,由茎叶图能得到中位数和甲、乙两人的最大速度等信息.
(2)由已知求出甲、乙两运动员的最大速度的平均数和方差,由乙的最大速度比甲稳定,得到派乙参加比赛更合适.
解答 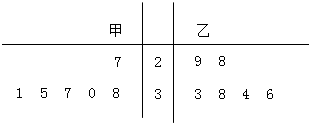 解:(1)由已知画茎叶图如右图,
解:(1)由已知画茎叶图如右图,
可以看出,甲、乙两人的最大速度都是均匀分布的,
只是甲的最大速度的中位数是33,乙的最大速度的中位数是33.5,
因此从中位数看乙的情况比甲好.
(2)$\overline{{x}_{甲}}$=$\frac{1}{6}$(27+38+30+37+35+31)=33,
$\overline{{x}_{乙}}$=$\frac{1}{6}$(33+29+38+34+28+36)=33,
所以他们的最大速度的平均数相同,
再看方差S2甲=$\frac{1}{6}$[(-6)2+…+(-2)2]=$\frac{47}{3}$,
S2乙=$\frac{1}{6}$(02+…+32)=$\frac{38}{3}$,则${{S}^{2}}_{甲}>{{S}^{2}}_{乙}$,
故乙的最大速度比甲稳定,所以派乙参加比赛更合适.
点评 本题考查茎叶图的画法及应用,考查平均数和方差的求法及应用,是基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{3}{2}$,1)和$\frac{19}{4}$ | B. | (3,2)和$\frac{\sqrt{19}}{2}$ | C. | (-$\frac{3}{2}$,1)和$\frac{\sqrt{19}}{2}$ | D. | ($\frac{3}{2}$,-1)和$\frac{\sqrt{19}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -1 | C. | 0 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2]∪[2,+∞) | B. | (-∞,0]∪[3,+∞) | C. | (-∞,1]∪[3,+∞) | D. | (-∞,1]∪[4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 关于直线x=$\frac{π}{12}$对称 | B. | 关于直线x=$\frac{5π}{12}$对称 | ||
| C. | 关于点($\frac{π}{12}$,0)对称 | D. | 关于点($\frac{5π}{12}$,0)对称 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com