练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图中，，，、分别是、的中点，将沿折起连结、，得到多面体.

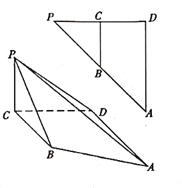
    （1）证明：在多面体中，；

    （2）在多面体中，当时，求二面角的余弦值.

    【答案】（1）见解析；（2）0.

    【解析】

    （1）根据线面垂直的判定定理，先得到平面，进而可得 ；

    （2）根据题意，先得到两两垂直，以为坐标原点，分别以为轴建立空间直角坐标系，求出两平面的法向量，根据向量夹角计算公式，即可求出结果.

    （1）证明：中，因为分别是的中点，

    所以，，

    所以多面体中， ，，

    又，平面；

    因为平面，

    （2）依题意可得， ，直角中，得，又

    所以，，

    由（1）知， ，平面

    以为坐标原点，分别以为轴，建立如图的坐标系.

    则，

    得

    设平面的一个法向量分别是，

    则可取.

    可取.

    .

    所以二面角的余弦值为0.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某商场为吸引顾客消费推出一项优惠活动．活动规则如下：消费额每满100元可转动如图所示的转盘一次，并获得相应金额的返券，假定指针等可能地停在任一位置.若指针停在A区域返券60元；停在B区域返券30元；停在C区域不返券.例如：消费218元，可转动转盘2次，所获得的返券金额是两次金额之和．

    （1）若某位顾客消费128元，求返券金额不低于30元的概率；

    （2）若某位顾客恰好消费280元，并按规则参与了活动，他获得返券的金额记为（元）．求随机变量的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知多面体ABCDEF中，四边形ABFE为正方形，，，G为AB的中点，.

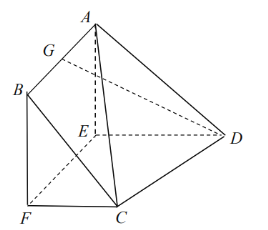
    （1）求证：平面CDEF；

    （2）求平面ACD与平面BCF所成锐二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某班50名学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].从样本成绩不低于80分的学生中随机选取2人,记这2人成绩在90分以上(含90分)的人数为ξ,则ξ的数学期望为( )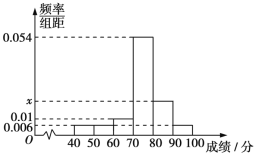

    A.B.C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，其中.

    （1）若为单调递减函数，求的取值范围；

    （2）若有两个不同的零点，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某市旅游管理部门为提升该市26个旅游景点的服务质量，对该市26个旅游景点的交通、安全、环保、卫生、管理五项指标进行评分，每项评分最低分0分，最高分100分，每个景点总分为这五项得分之和，根据考核评分结果，绘制交通得分与安全得分散点图、交通得分与景点总分散点图如下：

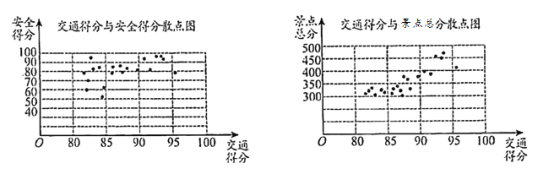
    请根据图中所提供的信息，完成下列问题：

    （I）若从交通得分前6名的景点中任取2个，求其安全得分都大于90分的概率；

    （II）若从景点总分排名前6名的景点中任取3个，记安全得分不大于90分的景点个数为，求随机变量的分布列和数学期望；

    （III）记该市26个景点的交通平均得分为安全平均得分为，写出和的大小关系？（只写出结果）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在四棱锥中，为等边三角形，四边形为矩形，为的中点，.

    证明：平面平面.

    设二面角的大小为，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，底面，四边形是菱形，点在线段上.

    （1）证明：平面平面；

    （2）若，二面角的余弦值为，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】过抛物线y2=4x的焦点的直线l与抛物线交于A，B两点，设点M（3，0）.若△MAB的面积为，则|AB|=( )

    A.2B.4C.D.8

    查看答案和解析>>

    同步练习册答案