
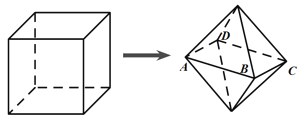
【题目】如图,棱长为1(单位:![]() )的正方体木块经过适当切割,得到几何体
)的正方体木块经过适当切割,得到几何体![]() ,已知几何体
,已知几何体![]() 由两个底面相同的正四棱锥组成,底面
由两个底面相同的正四棱锥组成,底面![]() 平行于正方体的下底面,且各顶点均在正方体的面上,则几何体
平行于正方体的下底面,且各顶点均在正方体的面上,则几何体![]() 体积的取值范围是________(单位:
体积的取值范围是________(单位:![]() ).
).
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】若关于x的不等式xex﹣2ax+a<0的非空解集中无整数解,则实数a的取值范围是( )
A.[ ![]() ,
, ![]() )
)
B.[ ![]() ,
, ![]() )
)
C.[ ![]() ,e]
,e]
D.[ ![]() ,e]
,e]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司在迎新年晚会上举行抽奖活动,有甲,乙两个抽奖方案供员工选择. 方案甲:员工最多有两次抽奖机会,每次抽奖的中奖率均为 ![]() ,第一次抽奖,若未中奖,则抽奖结束,若中奖,则通过抛一枚质地均匀的硬币,决定是否继续进行第二次抽奖,规定:若抛出硬币,反面朝上,员工则获得500元奖金,不进行第二次抽奖;若正面朝上,员工则须进行第二次抽奖,且在第二次抽奖中,若中奖,则获得1000元;若未中奖,则所获得奖金为0元.
,第一次抽奖,若未中奖,则抽奖结束,若中奖,则通过抛一枚质地均匀的硬币,决定是否继续进行第二次抽奖,规定:若抛出硬币,反面朝上,员工则获得500元奖金,不进行第二次抽奖;若正面朝上,员工则须进行第二次抽奖,且在第二次抽奖中,若中奖,则获得1000元;若未中奖,则所获得奖金为0元.
方案乙:员工连续三次抽奖,每次中奖率均为 ![]() ,每次中奖均可获得奖金400元.
,每次中奖均可获得奖金400元.
(Ⅰ)求某员工选择方案甲进行抽奖所获奖金X(元)的分布列;
(Ⅱ)试比较某员工选择方案乙与选择方案甲进行抽奖,哪个方案更划算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,四边形ABCD是矩形,E,M分别是AD,PD的中点,PE⊥BE,PA=PD=AD=2,AB=![]() .
.
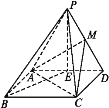
(1)求证:PB∥平面MAC.
(2)求证:平面MAC⊥平面PBE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 的图象向左平移
的图象向左平移![]() 个单位长度,再向上平移1个单位长度,得到函数g(x)的图象,则函数g(x)具有性质_____.(填入所有正确结论的序号)
个单位长度,再向上平移1个单位长度,得到函数g(x)的图象,则函数g(x)具有性质_____.(填入所有正确结论的序号)
①最大值为![]() ,图象关于直线
,图象关于直线![]() 对称;
对称;
②图象关于y轴对称;
③最小正周期为π;
④图象关于点![]() 对称.
对称.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列![]() 的前
的前![]() 项和为
项和为![]() ,公比
,公比![]() ,
,![]() ,
,![]() .
.
(1)求等比数列![]() 的通项公式;
的通项公式;
(2)设![]() ,求
,求![]() 的前
的前![]() 项和
项和![]() .
.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)将已知两式作差,利用等比数列的通项公式,可得公比,由等比数列的求和可得首项,进而得到所求通项公式;(2)求得bn=n,![]() ,由裂项相消求和可得答案.
,由裂项相消求和可得答案.
(1)等比数列![]() 的前
的前![]() 项和为
项和为![]() ,公比
,公比![]() ,
,![]() ①,
①,
![]() ②.
②.
②﹣①,得![]() ,则
,则![]() ,
,
又![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以![]() ,
,
所以![]() ;
;
(2)![]() ,
,![]()
所以前![]() 项和
项和![]() .
.
【点睛】
裂项相消法适用于形如 (其中
(其中![]() 是各项均不为零的等差数列,c为常数)的数列. 裂项相消法求和,常见的有相邻两项的裂项求和,还有一类隔一项的裂项求和,如
是各项均不为零的等差数列,c为常数)的数列. 裂项相消法求和,常见的有相邻两项的裂项求和,还有一类隔一项的裂项求和,如![]() 或
或![]() .
.
【题型】解答题
【结束】
22
【题目】已知函数![]() 的图象上有两点
的图象上有两点![]() ,
,![]() .函数
.函数![]() 满足
满足![]() ,且
,且![]() .
.
(1)求证:![]() ;
;
(2)求证:![]() ;
;
(3)能否保证![]() 和
和![]() 中至少有一个为正数?请证明你的结论.
中至少有一个为正数?请证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com