考点:轨迹方程,椭圆的标准方程,直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)求出椭圆的焦点,利用椭圆的定义,可得椭圆C
1的方程
(2)设Q(x,y),P(x
1,y
1),由题意,B(
,-1),利用点Q满足
•=0,
•=0,结合点P是椭圆C
1上异于点A,B的任意一点,求点Q的轨迹方程
(3)由于|AB|=2
,故Q到AB的距离最大时,△ABQ的面积最大,即可求△ABQ面积的最大值及此时点Q的坐标.
解答:
解:(1)双曲线C
2:
-y
2=1的顶点为F
1(-
,0),F
2(
,0),
∴椭圆C
1的焦点为F
1(-
,0),F
2(
,0),
∵椭圆过A(-
,1),
∴2a=|AF
1|+|AF
2|=4,
∴a=2,
∴b=
=
,
∴椭圆C
1的方程为
+=1;
(2)设Q(x,y),P(x
1,y
1)
由题意,B(
,-1),
∴
=(x+
,y-1),
=(x
1+
,y
1-1),
=(x-
,y+1),
=(x
1-
,y
1+1),
由
•=0,可得(x+
)(x
1+
)=-(y-1)(y
1-1),
•=0,可得(x-
)(x
1-
)=-(y+1)(y
1+1),
两式相乘,可得(x
2-2)(x
12-2)=(y
2-1)(y
12-1),
点P是椭圆C
1上异于点A,B的任意一点,∴x
12=4-2y
12,
∴-2(x
2-2)(y
12-2)=(y
2-1)(y
12-1),
y
12-1≠0时,2x
2+y
2=5;
y
12-1=0时,则P(-
,-1)或P(
,1),Q(
,1)或Q(-
,-1),满足2x
2+y
2=5,
P与A重合时,P(-
,1),
y=
x-3代入2x
2+y
2=5可得Q(
,-1)或(
,-2);
同理P与B重合时,Q(-
,1)或(-
,2);
∴Q的轨迹方程为2x
2+y
2=5,除去(
,-1)、(
,-2)、(-
,1)、(-
,2);
(3)由于|AB|=2
,故Q到AB的距离最大时,△ABQ的面积最大,
设与直线AB平行的直线为x+
y+m=0
与2x
2+y
2=5联立,可得5y
2+4
my+2c
2-5=0
△=32m
2-20(2m
2-5)=0,可得m=±
,
m=
,y=-2,x=-
;m=-
,y=2,x=
;
∴Q(
,2)或(-
,-2)时,△ABQ的面积最大,最大为
|AB|×
=
.
点评:本题考查椭圆的方程,考查直线与椭圆的位置关系,考查三角形面积的计算,考查学生分析解决问题的能力,有难度.



 中考解读考点精练系列答案
中考解读考点精练系列答案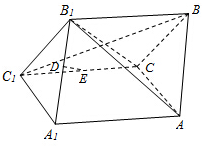 如图,四边形A A1 C1C为矩形,四边形CC1B1 B为菱形,且平面CC1B1 B⊥A A1 C1C,D,E分别是A1 B1和C1C的中点.求证:(1)BC1⊥平面AB1C;
如图,四边形A A1 C1C为矩形,四边形CC1B1 B为菱形,且平面CC1B1 B⊥A A1 C1C,D,E分别是A1 B1和C1C的中点.求证:(1)BC1⊥平面AB1C; 设α∈(0,π),且α≠
设α∈(0,π),且α≠