
【题目】如图,曲线C1是以原点O为中心,F1,F2为焦点的椭圆的一部分.曲线C2是以O为顶点,F2为焦点的抛物线的一部分,A是曲线C1和C2的交点且∠AF2F1为钝角,若|AF1|=![]() ,|AF2|=
,|AF2|=![]() .
.
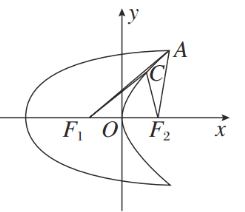
(1)求曲线C1和C2的方程;
(2)设点C是C2上一点,若|CF1|=![]() |CF2|,求△CF1F2的面积.
|CF2|,求△CF1F2的面积.
【答案】(1)曲线C1的方程为![]() +
+![]() =1(-3≤x≤
=1(-3≤x≤![]() ),曲线C2的方程为y2=4x(0≤x≤
),曲线C2的方程为y2=4x(0≤x≤![]() )
)
(2)2
【解析】(1)设椭圆方程为![]() +
+![]() =1(a>b>0),则2a=|AF1|+|AF2|=
=1(a>b>0),则2a=|AF1|+|AF2|=![]() +
+![]() =6,得a=3.
=6,得a=3.
设A(x,y),F1(-c,0),F2(c,0),则(x+c)2+y2=(![]() )2,(x-c)2+y2=(
)2,(x-c)2+y2=(![]() )2,两式相减得xc=
)2,两式相减得xc=![]() .由抛物线的定义可知|AF2|=x+c=
.由抛物线的定义可知|AF2|=x+c=![]() ,
,
则c=1,x=![]() 或x=1,c=
或x=1,c=![]() .又∠AF2F1为钝角,
.又∠AF2F1为钝角,
则x=1,c=![]() 不合题意,舍去.当c=1时,b=2
不合题意,舍去.当c=1时,b=2![]() ,
,
所以曲线C1的方程为![]() +
+![]() =1(-3≤x≤
=1(-3≤x≤![]() ),曲线C2的方程为y2=4x(0≤x≤
),曲线C2的方程为y2=4x(0≤x≤![]() ).
).
(2)过点F1作直线l垂直于x轴,过点C作CC1⊥l于点C1,依题意知|CC1|=|CF2|.
在Rt△CC1F1中,|CF1|=![]() |CF2|=
|CF2|=![]() |CC1|,所以∠C1CF1=45°,
|CC1|,所以∠C1CF1=45°,
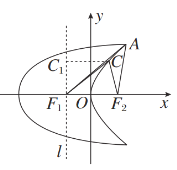
所以∠CF1F2=∠C1CF1=45°.
在△CF1F2中,设|CF2|=r,则|CF1|=![]() r,|F1F2|=2.
r,|F1F2|=2.
由余弦定理得22+(![]() r)2-2×2×
r)2-2×2×![]() rcos45°=r2,
rcos45°=r2,
解得r=2,
所以△CF1F2的面积S△CF1F2=![]() |F1F2|·|CF1|sin45°=
|F1F2|·|CF1|sin45°=![]() ×2×2
×2×2![]() sin45°=2.
sin45°=2.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,
, ![]() 上的动点
上的动点![]() 到两焦点的距离之和为4,当点
到两焦点的距离之和为4,当点![]() 运动到椭圆
运动到椭圆![]() 的上顶点时,直线
的上顶点时,直线![]() 恰与以原点
恰与以原点![]() 为圆心,以椭圆
为圆心,以椭圆![]() 的离心率为半径的圆相切.
的离心率为半径的圆相切.
(1)求椭圆![]() 的方程;
的方程;
(2)设椭圆![]() 的左右顶点分别为
的左右顶点分别为![]() ,若
,若![]() 交直线
交直线![]() 于
于![]() 两点.问以
两点.问以![]() 为直径的圆是否过定点?若过定点,请求出该定点坐标;若不过定点,请说明理由.
为直径的圆是否过定点?若过定点,请求出该定点坐标;若不过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知由自然数组成的![]() 元集合
元集合![]() ,非空集合
,非空集合![]() ,且对任意的
,且对任意的![]() ,都有
,都有![]() .
.
(1)当![]() 时,求所有满足条件的集合
时,求所有满足条件的集合![]() ;
;
(2)当![]() 时,求所有满足条件的集合
时,求所有满足条件的集合![]() 的元素总和;
的元素总和;
(3)定义一个集合的“交替和”如下:按照递减的次序重新排列该集合的元素,然后从最大数开始交替地减、加后继的数.例如集合![]() 的交替和是
的交替和是![]() ,集合
,集合![]() 的交替和为
的交替和为![]() .当
.当![]() 时,求所有满足条件的集合
时,求所有满足条件的集合![]() 的“交替和”的总和.
的“交替和”的总和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层。某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元。该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)=![]() 若不建隔热层,每年能源消耗费用为8万元。设f(x)为隔热层建造费用与20年的能源消耗费用之和。
若不建隔热层,每年能源消耗费用为8万元。设f(x)为隔热层建造费用与20年的能源消耗费用之和。
(Ⅰ)求k的值及f(x)的表达式。
(Ⅱ)隔热层修建多厚时,总费用f(x)达到最小,并求最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]()
![]()
![]() ,若
,若![]() ,且
,且![]() 的图象相邻的对称轴间的距离不小于
的图象相邻的对称轴间的距离不小于![]() .
.
(1)求![]() 的取值范围.
的取值范围.
(2)若当![]() 取最大值时,
取最大值时, ![]() ,且在
,且在![]() 中,
中, ![]() 分别是角
分别是角![]() 的对边,其面积
的对边,其面积![]() ,求
,求![]() 周长的最小值.
周长的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)求函数![]() 在区间
在区间![]() 上的值域
上的值域
(2)把函数![]() 图象所有点的上横坐标缩短为原来的
图象所有点的上横坐标缩短为原来的![]() 倍,再把所得的图象向左平移
倍,再把所得的图象向左平移![]() 个单位长度
个单位长度![]() ,再把所得的图象向下平移1个单位长度,得到函数
,再把所得的图象向下平移1个单位长度,得到函数![]() , 若函数
, 若函数![]() 关于点
关于点![]() 对称
对称
(i)求函数![]() 的解析式;
的解析式;
(ii)求函数![]() 单调递增区间及对称轴方程.
单调递增区间及对称轴方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com