
【题目】已知数列![]() 满足
满足![]() ,且
,且![]() .
.
(Ⅰ)求![]() ,
,![]() 的值;
的值;
(Ⅱ)是否存在实数![]() ,
,![]() ,使得
,使得 ,对任意正整数
,对任意正整数![]() 恒成立?若存在,求出实数
恒成立?若存在,求出实数![]() 、
、![]() 的值并证明你的结论;若不存在,请说明理由.
的值并证明你的结论;若不存在,请说明理由.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】三角形的三个顶点的坐标分别为![]() ,
,![]() ,
,![]() ,则该三角形的重心(三边中线交点)的坐标为
,则该三角形的重心(三边中线交点)的坐标为![]() .类比这个结论,连接四面体的一个顶点及其对面三角形重心的线段称为四面体的中线,四面体的四条中线交于一点,该点称为四面体的重心.若四面体的四个顶点的空间坐标分别为
.类比这个结论,连接四面体的一个顶点及其对面三角形重心的线段称为四面体的中线,四面体的四条中线交于一点,该点称为四面体的重心.若四面体的四个顶点的空间坐标分别为![]() ,
,![]() ,
,![]() ,
,![]() ,则该四面体的重心的坐标为( )
,则该四面体的重心的坐标为( )
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着生活节奏的加快以及智能手机的普及,外卖点餐逐渐成为越来越多用户的餐饮消费习惯.由此催生了一批外卖点餐平台,已知某外卖平台的送餐费用与送餐距离有关(该平台只给5千米范围内配送),为调査送餐员的送餐收入,现从该平台随机抽取80名点外卖的用户进行统计,按送餐距离分类统计结果如下表:

以这80名用户送餐距离位于各区间的频率代替送餐距离位于该区间的概率.
(1)从这80名点外卖的用户中任取一名用户.求该用户的送餐距离不超过3千米的概率;
(2)试估计利用该平台点外卖用户的平均送餐距离;
(3)若该外卖平台给送餐员的送餐贽用与送餐距离有关,规定2千米内为短距离,每份3元,2千米到4千米为中距离,每份5元;超过4千米为远距离,每份9元,若送餐员一天的目标收 人不低于150元,试估计一天至少要送多少份外卖?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代中的“礼、乐、射、御、书、数”合称“六艺”.“礼”,主要指德育;“乐”,主要指美育;“射”和“御”,就是体育和劳动;“书”,指各种历史文化知识;“数”,指数学.某校国学社团开展“六艺”课程讲座活动,每艺安排一节,连排六节,一天课程讲座排课有如下要求:“数”必须排在第三节,且“射”和“御”两门课程相邻排课,则“六艺”课程讲座不同的排课顺序共有( )
A.12种B.24种C.36种D.48种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是线段
是线段![]() 上靠近点
上靠近点![]() 的一个三等分点,点
的一个三等分点,点![]() 是线段
是线段![]() 上的一个动点,且
上的一个动点,且![]() .如图,将
.如图,将![]() 沿
沿![]() 折起至
折起至![]() ,使得平面
,使得平面![]() 平面
平面![]() .
.
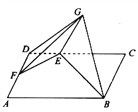
(1)当![]() 时,求证:
时,求证:![]() ;
;
(2)是否存在![]() ,使得
,使得![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】祖暅(公元前5~6世纪)是我国齐梁时代的数学家,是祖冲之的儿子,他提出了一条原原理:“幂势既同,则积不容异.”这里的“幂”指水平截面的面积,“势”指高。这句话的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体体积相等。设由椭圆![]() 所围成的平面图形绕
所围成的平面图形绕![]() 轴旋转一周后,得一橄榄状的几何体(称为椭球体),课本中介绍了应用祖暅原理求球体体积公式的做法,请类比此法,求出椭球体体积,其体积等于( )
轴旋转一周后,得一橄榄状的几何体(称为椭球体),课本中介绍了应用祖暅原理求球体体积公式的做法,请类比此法,求出椭球体体积,其体积等于( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北京是我国严重缺水的城市之一.为了倡导“节约用水,从我做起”,小明在他所在学校的2000名同学中,随机调查了40名同学家庭中一年的月均用水量(单位:吨),并将月均用水量分为6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 加以统计,得到如图所示的频率分布直方图.
加以统计,得到如图所示的频率分布直方图.
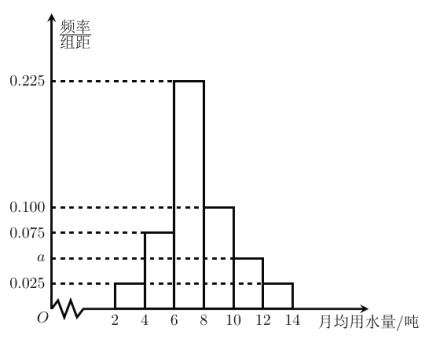
(1)给出图中实数a的值;
(2)根据样本数据,估计小明所在学校2000名同学家庭中,月均用水量低于8吨的约有多少户;
(3)在月均用水量大于或等于10吨的样本数据中,小明决定随机抽取2名同学家庭进行访谈,求这2名同学中恰有1人所在家庭的月均用水量属于![]() 组的概率.
组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电动车售后服务调研小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于50公里和300公里之间,将统计结果分成5组:![]() ,绘制成如图所示的频率分布直方图.
,绘制成如图所示的频率分布直方图.

(1)求续驶里程在![]() 的车辆数;
的车辆数;
(2)求续驶里程的平均数;
(3)若从续驶里程在![]() 的车辆中随机抽取2辆车,求其中恰有一辆车的续驶里程在
的车辆中随机抽取2辆车,求其中恰有一辆车的续驶里程在![]() 内的概率.
内的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com