
分析 先根据向量$\overrightarrow{OA},\overrightarrow{OB}$的坐标,求出$|\overrightarrow{OA}|=3,|\overrightarrow{OB}|=5$,从而得到$\overrightarrow{OC}=(\frac{4}{5},λ+\frac{3}{5})$,根据向量长度$|\overrightarrow{OC}|=\sqrt{5}$,即可得到$5=(\frac{4}{5})^{2}+(λ+\frac{3}{5})^{2}$,解该方程,并取λ>0解,这样即可得出$\overrightarrow{OC}$的坐标,从而得出点C的坐标.
解答 解:根据条件,$|\overrightarrow{OA}|=3,|\overrightarrow{OB}|=5$;
∴$\overrightarrow{OC}=\frac{λ}{3}•(0,3)+\frac{1}{5}•(4,3)=(\frac{4}{5},λ+\frac{3}{5})$;
又$|\overrightarrow{OC}|=\sqrt{5}$;
∴${\overrightarrow{OC}}^{2}=\frac{16}{25}+{λ}^{2}+\frac{6}{5}λ+\frac{9}{25}=5$;
解得$λ=\frac{-3±\sqrt{109}}{5}$;
∵λ>0;
∴$λ=\frac{-3+\sqrt{109}}{5}$;
∴$\overrightarrow{OC}=(\frac{4}{5},\frac{\sqrt{109}}{5})$;
∴C点的坐标为($\frac{4}{5},\frac{\sqrt{109}}{5}$).
故答案为:($\frac{4}{5}$,$\frac{\sqrt{109}}{5}$).
点评 考查根据向量的坐标求向量的长度,向量坐标的数乘即加法运算,数量积的坐标运算,以及解一元二次方程,清楚向量坐标和对应点的坐标的关系.


科目:高中数学 来源: 题型:解答题
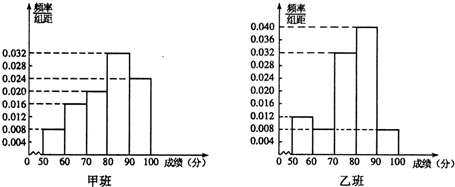
| 甲班(A方式) | 乙班(B方式) | 总计 | |
| 成绩优秀 | |||
| 成绩不优秀 | |||
| 总计 |
| P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 概率 事件 | 甲胜乙 | 甲平乙 | 甲输乙 |
| 概率 | $\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{3}$ |
| 概率 事件 | 甲胜丙 | 甲平丙 | 甲输丙 |
| 概率 | $\frac{2}{3}$ | $\frac{1}{6}$ | $\frac{1}{6}$ |
| 概率 事件 | 乙胜丙 | 乙平丙 | 乙输丙 |
| 概率 | $\frac{2}{3}$ | $\frac{1}{6}$ | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ①③ | C. | ②④ | D. | ②③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com