
分析 (1)根据题意,得出今后每年的旅游业收人组成等比数列,求出前n项和即可;
(2)令前n项和Sn≥8000,求出满足条件的n值即可.
解答 解:(1)根据题意,得;
今后每年的旅游业收人组成等比数列,
且首项为a1=400,公比q=$\frac{5}{4}$,
∴n年内旅游业的总收人为
Sn=$\frac{{a}_{1}(1{-q}^{n})}{1-q}$
=$\frac{400(1{-(\frac{5}{4})}^{n})}{1-\frac{5}{4}}$
=1600[${(\frac{5}{4})}^{n}$-1];
(2)令Sn≥8000,
即1600[${(\frac{5}{4})}^{n}$-1]≥8000,
即${(\frac{5}{4})}^{n}$≥6,
∴n≥${log}_{\frac{5}{4}}$6=$\frac{lg6}{lg\frac{5}{4}}$
=$\frac{lg2+lg3}{lg5-lg4}$
=$\frac{lg2+lg3}{1-3lg2}$
=$\frac{0.301+0.477}{1-3×0.301}$≈8;
∴估计大约8年后,旅游业的总收入超过8000万元.
点评 本题考查了等比数列的通项公式与前n项和公式的应用问题,是基础题目.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:高中数学 来源: 题型:选择题
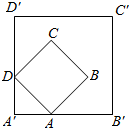 如图所示,边长为1的正方形ABCD的顶点A,D分别在边长为2的正方形A′B′C′D′的边A′B′和A′D′上移动,则$\overrightarrow{A'B}•\overrightarrow{A'C}$的最大值是( )
如图所示,边长为1的正方形ABCD的顶点A,D分别在边长为2的正方形A′B′C′D′的边A′B′和A′D′上移动,则$\overrightarrow{A'B}•\overrightarrow{A'C}$的最大值是( )| A. | 2 | B. | 1+$\sqrt{2}$ | C. | π | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com